Hilbert's paradox of the Grand Hotel facts for kids

Hilbert's paradox of the Grand Hotel is a math idea named after David Hilbert, a German mathematician. It's called a paradox because it shows something that seems impossible but is actually true. Hilbert used this idea to explain how infinity works differently from normal numbers.

The Grand Hotel Paradox

Imagine a normal hotel. It has a set number of rooms, like 100 rooms. If all 100 rooms are full, the hotel can't take any new guests. It's completely booked!

Now, let's think about a very special hotel. This hotel has an infinite number of rooms. The rooms are numbered 1, 2, 3, and so on, forever.

What if this infinite hotel is completely full? Every single room has a guest. It might seem like no new guests can check in, just like a normal hotel. But this is where the paradox begins!

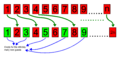
Adding One New Guest

Even if the infinite hotel is full, it can still make room for a new guest. Here's how:

• The guest in room 1 moves to room 2.
• The guest in room 2 moves to room 3.
• The guest in room 3 moves to room 4.
• This keeps going for every guest. The guest in room n moves to room n+1.

After everyone moves, room 1 becomes empty! The new guest can now check into room 1. This shows that in an infinite hotel, "full" doesn't mean the same thing as in a normal hotel. You can always find space, even if it seems full.

Welcoming Infinite New Guests

The Grand Hotel can do even more amazing things. What if an entire bus full of new guests arrives, and there are an infinite number of people on the bus? Can the hotel make room for them, even if it's already full? Yes!

Here's how the hotel can fit an infinite number of new guests:

• Each guest already in the hotel needs to move.
• They move to a new room by multiplying their current room number by two.
• So, the guest in room 1 moves to room 2 (1 x 2).
• The guest in room 2 moves to room 4 (2 x 2).
• The guest in room 3 moves to room 6 (3 x 2).
• In general, the guest in room n moves to room 2n.

After all the original guests move, all the rooms with odd numbers (like 1, 3, 5, 7...) become empty! Since there are an infinite number of odd numbers, this means there are an infinite number of empty rooms. The infinite number of new guests can then check into these empty odd-numbered rooms.

This shows that an infinite hotel can double its number of guests without getting any bigger. It's a strange idea, but it helps us understand how infinity works in mathematics. It's not a real paradox that breaks rules, but rather a way to show how our normal ideas about numbers don't always apply to infinity.

Images for kids

• 

  Hilbert's Hotel

See also

In Spanish: El hotel infinito de Hilbert para niños