Zermelo–Fraenkel set theory Facts for Kids

Zermelo–Fraenkel set theory (often called ZF) is a special set of rules, known as axioms. These rules help mathematicians work with set theory in a clear and logical way. When another important rule, called the axiom of choice, is added to ZF, the system becomes ZFC. Most mathematicians today use ZFC to understand and build upon set theory.

Mathematicians needed these rules after a problem called Russell's paradox was discovered in 1901. This problem showed that some ideas about sets could lead to contradictions. To fix this, Ernst Zermelo suggested a set theory in 1908. Later, in 1922, Abraham Fraenkel improved Zermelo's ideas, leading to the system we use today.

What Are Axioms?
The Axiom of Choice
See also

What Are Axioms?

An axiom is a basic statement or rule that is accepted as true without needing a proof. Think of them as the starting points or fundamental truths in a mathematical system. Zermelo–Fraenkel set theory (ZF) has eight main axioms.

Axiom of Extension

This axiom says that two sets are exactly the same if and only if they have all the same elements. The order of the elements does not matter.

For example, the set 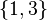$\{1, 3\}$ and the set 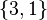$\{3, 1\}$ are considered equal.

Axiom of Foundation

This rule states that every set (except for the empty set, which has no elements) must contain at least one element that is completely separate from it. This means that element shares no members with the original set. This helps prevent sets from containing themselves in strange ways.

Axiom of Specification

This axiom lets us create new sets from existing ones. If you have a set 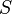$S$ and a rule 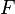$F$ (a function that is either true or false for each element), this axiom says that a new set exists. This new set contains only the elements from 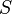$S$ for which the rule 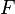$F$ is true.

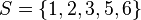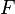For example, if $S = \{1, 2, 3, 5, 6\}$ , and $F$ is "this is an even number", then this axiom guarantees that the set 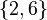$\{2, 6\}$ exists.

Axiom of Pairing

This axiom is simple: if you have any two sets, this rule says that you can always create a new set that contains exactly those two original sets as its only members.

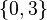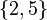For example, if you have the sets $\{0, 3\}$ and $\{2, 5\}$ , this axiom says that the set $\{\{0, 3\}, \{2, 5\}\}$ exists.

Axiom of Union

The axiom of union allows you to combine elements from different sets. If you have a set of sets, this axiom says that there is another set that contains all the individual elements from all those inner sets.

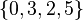For example, given the set $\{\{0, 3\}, \{2, 5\}\}$ , this axiom says that the set $\{0, 3, 2, 5\}$ exists. It combines all the numbers from inside the smaller sets.

Axiom of Replacement

This axiom is about changing elements in a set. If you have a set 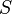$S$ and a rule 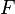$F$ that changes each element (like a mathematical function), this axiom says that a new set exists. This new set contains all the results of applying the rule 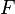$F$ to every member of the original set $S$ .

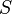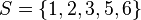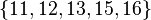For example, if $S = \{1, 2, 3, 5, 6\}$ and $F$ is "add ten to this number", then the axiom says that the set $\{11, 12, 13, 15, 16\}$ exists.

Axiom of Infinity

This axiom is important because it guarantees the existence of infinite sets. It specifically says that the set of all natural numbers (like 0, 1, 2, 3, and so on) exists. This set is often defined using a special mathematical construction.

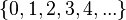This is the set $\{0, 1, 2, 3, 4, ...\}$ .

Axiom of Power Set

This axiom states that for any given set, there always exists a "power set." A power set is a set that contains all possible subsets of the original set. This includes the empty set and the original set itself.

For example, the power set of 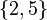$\{2, 5\}$ is $\{\{\}, \{2\}, \{5\}, \{2, 5\}\}$ .

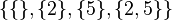The Axiom of Choice

The axiom of choice is an extra rule that is often added to ZF to create ZFC. It says that if you have a collection of non-empty sets, you can always create a new set by picking exactly one element from each of those sets.

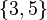For example, given the set $\{\{0, 3\}, \{2, 5\}\}$ , the axiom of choice would show that a set like $\{3, 5\}$ can be formed by picking one element from each inner set.

For sets that have a limited number of elements (finite sets), you can usually prove this axiom using the other rules. However, for sets with an unlimited number of elements (infinite sets), you cannot prove it from the other axioms alone. This is why it is considered a separate, important axiom.

Zermelo–Fraenkel set theory facts for kids

Contents