Axiom of choice facts for kids
The axiom of choice, often called AC, is a special rule in mathematics. It is used in a field called set theory. Imagine you have many groups of things. Each group has at least one item. The axiom of choice says you can always pick one item from each group. Then, you can make a new group with all your chosen items.
You don't always need this rule. If you have a limited number of groups, you can just pick one item from each. You also don't need it if there's a clear rule for picking. For example, if you have many pairs of shoes, you can always pick the left shoe from each pair. But if you have an infinite collection of pairs of socks, and no way to tell them apart, the axiom of choice helps you pick one from each pair.
Contents
What is the Axiom of Choice?
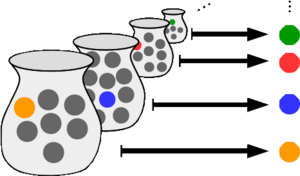
The axiom of choice is a basic idea, or axiom, in set theory. Set theory is a branch of mathematics that studies collections of objects. The axiom helps mathematicians work with very large, even infinite, collections of things. It states that if you have a collection of non-empty sets, you can always create a new set. This new set will contain exactly one item from each of the original sets.
Why is it an Axiom?
An axiom is like a starting rule that we accept as true without proof. We need axioms to build up mathematical theories. The axiom of choice is special because it's not always obvious that such a choice is possible, especially with infinite sets. For example, if you have an infinite number of jars, and each jar has at least one marble, the axiom says you can always pick one marble from every jar.
When Do We Use It?
Mathematicians use the axiom of choice in many areas. It helps them prove important theorems in fields like analysis and topology. These are advanced parts of mathematics. Without the axiom of choice, some very common and useful mathematical ideas would not work.
Finite vs. Infinite Choices
When you have a limited number of sets, picking one item from each is easy. You can just go through them one by one. This is called a finite number of sets.
However, when you have an infinite number of sets, it gets tricky. If there's no clear rule to pick an item from each set, you can't just list your choices. This is where the axiom of choice becomes important. It gives mathematicians permission to make these choices, even if they can't describe exactly how to make them.
The Sock and Shoe Example
Think about shoes. If you have many pairs of shoes, you can easily pick the left shoe from every pair. There's a clear rule: "pick the left one." You don't need the axiom of choice for this.
Now, imagine you have an infinite number of pairs of socks. These socks are all identical. You can't tell a "left" sock from a "right" sock. There's no rule like "pick the left sock" because they look the same. In this case, to pick one sock from each pair, mathematicians use the axiom of choice. It allows them to say, "Yes, it's possible to make such a collection of choices," even without a specific rule.
See also
 In Spanish: Axioma de elección para niños
In Spanish: Axioma de elección para niños