Perfect number facts for kids

This picture shows how the number 6 is a perfect number. If you add its parts (1, 2, and 3), you get 6!

A perfect number is a special kind of number. Imagine you have a number, and you find all the numbers that divide into it evenly (these are called its divisors). If you add up all these divisors, but you don't include the number itself, and the total equals the original number, then it's a perfect number! It's like the number is "perfectly balanced" by its parts.

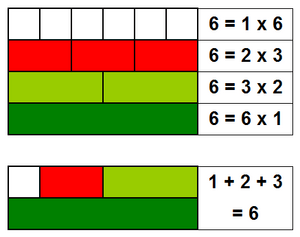
The first perfect number you'll find is 6. Let's see why:

• The numbers that divide into 6 evenly are 1, 2, 3, and 6.
• If we take out 6 itself, we are left with 1, 2, and 3.
• Add them up: 1 + 2 + 3 = 6.

Since the sum is 6, the number 6 is a perfect number!

The next perfect number is 28. Can you guess its divisors?

• The numbers that divide into 28 are 1, 2, 4, 7, 14, and 28.
• If we don't count 28, we have 1, 2, 4, 7, and 14.
• Add them together: 1 + 2 + 4 + 7 + 14 = 28.

So, 28 is also a perfect number!

The first four perfect numbers are 6, 28, 496, and 8128. These numbers have fascinated mathematicians for thousands of years!

What Makes a Number Perfect?

Perfect numbers are quite rare. They are connected to another special type of number called Mersenne primes. A Mersenne prime is a prime number that is one less than a power of two. For example, 3 is a Mersenne prime because it's 2² - 1. 7 is also a Mersenne prime (2³ - 1).

Euclid's Discovery

About 2,300 years ago, a famous Greek mathematician named Euclid discovered a rule for finding perfect numbers. He found that if you have a Mersenne prime, you can use it to create a perfect number.

• Euclid's rule says: If (2^p - 1) is a prime number (a Mersenne prime), then 2^(p-1) * (2^p - 1) will be a perfect number.
• Here, 'p' must also be a prime number.

Let's try Euclid's rule with an example:

• If p = 2, then (2² - 1) = 3, which is a prime number.
• Using the rule: 2^(2-1) * (2² - 1) = 2¹ * 3 = 2 * 3 = 6.
• And 6 is our first perfect number!

Let's try another one:

• If p = 3, then (2³ - 1) = 7, which is also a prime number.
• Using the rule: 2^(3-1) * (2³ - 1) = 2² * 7 = 4 * 7 = 28.
• And 28 is our second perfect number!

This rule works for all the perfect numbers we know so far.

Even and Odd Perfect Numbers

All the perfect numbers discovered so far are even numbers. No one has ever found an odd perfect number.

The Search for Odd Perfect Numbers

Mathematicians have been looking for an odd perfect number for a very long time. It's one of the oldest unsolved problems in number theory.

• If an odd perfect number exists, it would have to be very, very large.
• It would also need to have at least nine different prime factors.
• Even with powerful computers, no odd perfect number has been found yet.

This mystery keeps mathematicians busy! They continue to explore numbers, hoping to either find an odd perfect number or prove that they don't exist.

How Many Perfect Numbers Are There?

We don't know how many perfect numbers exist in total. We only know as many as we've been able to find.

• As of 2024, 52 perfect numbers have been discovered.
• Each new perfect number found is much larger than the last one.
• The search for new perfect numbers often involves finding new Mersenne primes, which are also very rare.

The largest known perfect number has millions of digits! It's truly amazing how these special numbers keep appearing in the vast world of mathematics.

See also

In Spanish: Número perfecto para niños