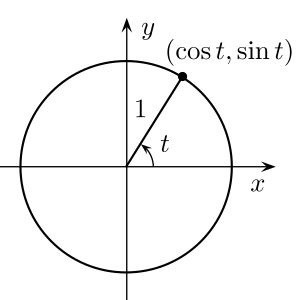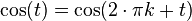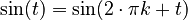Unit circle facts for kids
In mathematics, a unit circle is a special circle. It has a radius of exactly 1 unit. Imagine a circle drawn on a graph. Its center is right at the middle, where the X and Y axes cross (this point is called the Origin, or (0,0)).
The equation that describes every point on this circle is 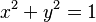 . This simple circle is super useful in a branch of math called Trigonometry.
. This simple circle is super useful in a branch of math called Trigonometry.
Contents
How Does the Unit Circle Help with Trigonometry?
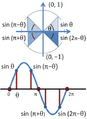
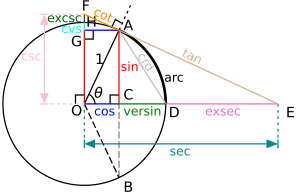
The unit circle makes understanding Trigonometric functions much easier. Imagine a line starting from the center of the circle (0,0) and going out to any point on the circle's edge. This line forms an angle with the positive X-axis. Let's call this angle t.
- The x-coordinate of the point where the line touches the circle is called the cosine of the angle t. We write this as
 .
. - The y-coordinate of the same point is called the sine of the angle t. We write this as
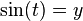 .
.
Since we know the equation of the unit circle is 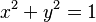 , we can replace x with
, we can replace x with 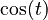 and y with
and y with 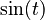 . This gives us a very important trigonometric equation:
. This gives us a very important trigonometric equation: 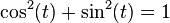 . This equation is always true for any angle t!
. This equation is always true for any angle t!
Understanding Angles on the Unit Circle
When you first learn about trigonometry, you often work with angles between 0 and 90 degrees. On the unit circle, these angles are in the top-right quarter. However, the unit circle lets us work with any angle, even angles larger than 90 degrees or negative angles.
The unit circle also shows us something cool about angles that repeat. If you go around the circle one full turn (which is 360 degrees or 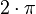 radians), you end up at the same spot. This means the sine and cosine values will be the same.
radians), you end up at the same spot. This means the sine and cosine values will be the same.
So, for any integer (whole number) k:
This means adding or subtracting full circles (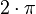 radians or 360 degrees) to an angle doesn't change its sine or cosine value.
radians or 360 degrees) to an angle doesn't change its sine or cosine value.
Images for kids
See also
 In Spanish: Circunferencia goniométrica para niños
In Spanish: Circunferencia goniométrica para niños