Euler–Mascheroni constant facts for kids
The Euler-Mascheroni constant is a special number in mathematics. It shows up in areas like analysis and number theory. This constant was first discovered by the Swiss mathematician Leonhard Euler in the early 1700s.
It is usually shown with the Greek letter 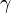 (which is pronounced "gamma"). However, Euler himself used the letters C and O for it.
(which is pronounced "gamma"). However, Euler himself used the letters C and O for it.
Scientists are still not sure if this number is irrational or transcendental. An irrational number cannot be written as a simple fraction. A transcendental number cannot be the solution to a simple equation called a polynomial with whole number parts.
The value of 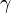 is about
is about 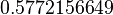 . An Italian mathematician named Lorenzo Mascheroni also worked with this number. He tried to find its value with many decimal places but made a few small mistakes.
. An Italian mathematician named Lorenzo Mascheroni also worked with this number. He tried to find its value with many decimal places but made a few small mistakes.
What Makes It Special?
The Euler-Mascheroni constant is important because it connects two different math ideas. It links the harmonic series with the natural logarithm.
The harmonic series is a list of fractions added together, like 1 + 1/2 + 1/3 + 1/4 and so on. This series keeps growing and growing without end. The natural logarithm is a special type of logarithm often used in science.
The constant is defined as the difference between the sum of the harmonic series and the natural logarithm of a very large number. Imagine you add up many terms of the harmonic series. Then, you subtract the natural logarithm of that same large number. As the number gets bigger and bigger, this difference gets closer and closer to the Euler-Mascheroni constant.
How Is It Defined?
Mathematicians can define the Euler-Mascheroni constant in a few ways. One way is using a "limit." A limit is what a value gets closer and closer to as something else changes.
It can also be defined using an "improper integral." This is a type of math problem that involves finding the area under a curve that goes on forever. It uses something called the floor function. The floor function simply gives you the largest whole number that is less than or equal to a given number. For example, the floor of 3.7 is 3.
The gamma constant is also connected to another important math function called the Gamma function. It's specifically linked to how the Gamma function changes, which is called its "derivative."
Related pages
- Divisor function
Images for kids
See also
 In Spanish: Constante de Euler-Mascheroni para niños
In Spanish: Constante de Euler-Mascheroni para niños

