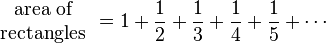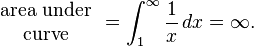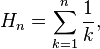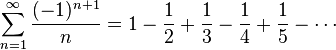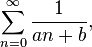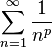Harmonic series (mathematics) facts for kids
The harmonic series is a special kind of math puzzle. Imagine you have a list of fractions: 1, then 1/2, then 1/3, then 1/4, and so on. The harmonic series is what you get when you add all these fractions together, forever!
This series is called "infinite" because you can always add another fraction to it. There's no end to the list.
It's also called "divergent." This means that even though the fractions you're adding get smaller and smaller, the total sum never stops growing. It just keeps getting bigger and bigger, without ever reaching a final number.
The name "harmonic" comes from music. When a string vibrates, it creates sounds called harmonics. The lengths of the waves for these sounds are related to the fractions 1/2, 1/3, 1/4, and so on, compared to the main sound wave. Also, in the series, each number (after the first one) is the "harmonic mean" of the numbers next to it.
Contents
History of the Harmonic Series
People have known about the harmonic series for a long time. The idea that this series keeps growing forever was first shown in the 1300s by a smart person named Nicole Oresme. But his discovery was forgotten for a while.
Later, in the 1600s, other mathematicians like Pietro Mengoli, Johann Bernoulli, and Jacob Bernoulli proved it again.
Harmonic patterns have also been used in architecture. During the Baroque period, architects used these patterns to design the sizes and shapes of floor plans, elevations, and even small details in churches and palaces.
Why the Harmonic Series Diverges
It might seem strange that adding smaller and smaller numbers can still lead to an endlessly growing sum. But there are a few ways to show why the harmonic series is divergent.
Comparing Numbers
One way to see why the harmonic series grows forever is to compare it to another series. Let's look at the harmonic series:
Now, let's make a new series where we replace some fractions with smaller ones, specifically using powers of two in the bottom number (denominator):
Notice that each fraction in the harmonic series is either bigger than or equal to the fraction in the new series. For example, 1/3 is bigger than 1/4, and 1/5 is bigger than 1/8.
Now, let's group the terms in the new series:
When you group them like this, you see that each group adds up to 1/2. Since there are infinitely many such groups, the sum of this new series is 1 + 1/2 + 1/2 + 1/2 + ... which clearly goes on forever.
Since the harmonic series is always bigger than or equal to this new series (which goes to infinity), the harmonic series must also go to infinity! This clever proof was first thought up by Nicole Oresme around 1350.
Using Areas (Integral Test)
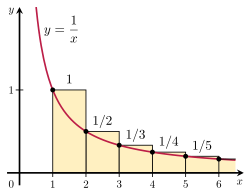
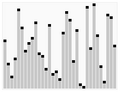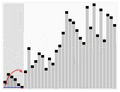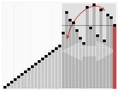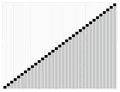
Another way to prove the harmonic series diverges is by looking at areas. Imagine drawing a graph. We can draw rectangles that have a width of 1 and a height equal to each term in the harmonic series (1, 1/2, 1/3, etc.).
The total area of all these rectangles added together would be the sum of the harmonic series:
Now, imagine a smooth curve on the same graph, called y = 1x. If you calculate the area under this curve from 1 to infinity, it also turns out to be infinite. This is called an improper integral.
Looking at the picture, you can see that the area of all the rectangles completely covers the area under the curve. Since the area under the curve is infinite, the total area of the rectangles (which is the harmonic series) must also be infinite.
How Fast Does It Grow?
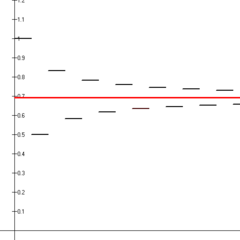
The harmonic series grows very, very slowly. For example, you would have to add up more than 1043 terms (that's a 1 with 43 zeros after it!) before the sum even reaches 100. This slow growth is because the sum increases in a way that's related to logarithms.
Mathematician Leonhard Euler showed that the sum of the first k terms of the harmonic series is roughly equal to the natural logarithm of k plus a special number called the Euler–Mascheroni constant.
Partial Sums (Harmonic Numbers)
When you add up only a certain number of terms from the harmonic series, you get what are called harmonic numbers. We write this as Hn, where n is how many terms you've added.
For example:
- H1 = 1
- H2 = 1 + 1/2 = 1.5
- H3 = 1 + 1/2 + 1/3 = 11/6 ≈ 1.833
The only harmonic number that is a whole number is H1 = 1. All other harmonic numbers are fractions or decimals.
| n | Partial sum of the harmonic series, Hn | |||
|---|---|---|---|---|
| expressed as a fraction | decimal | relative size | ||
| 1 | 1 | 1 |
|
|
| 2 | 3 | /2 | 1.5 |
|
| 3 | 11 | /6 | ~1.83333 |
|
| 4 | 25 | /12 | ~2.08333 |
|
| 5 | 137 | /60 | ~2.28333 |
|
| 6 | 49 | /20 | 2.45 |
|
| 7 | 363 | /140 | ~2.59286 |
|
| 8 | 761 | /280 | ~2.71786 |
|
| 9 | 7129 | /2520 | ~2.82897 |
|
| 10 | 7381 | /2520 | ~2.92897 |
|
| 11 | 83711 | /27720 | ~3.01988 |
|
| 12 | 86021 | /27720 | ~3.10321 |
|
| 13 | 1145993 | /360360 | ~3.18013 |
|
| 14 | 1171733 | /360360 | ~3.25156 |
|
| 15 | 1195757 | /360360 | ~3.31823 |
|
| 16 | 2436559 | /720720 | ~3.38073 |
|
| 17 | 42142223 | /12252240 | ~3.43955 |
|
| 18 | 14274301 | /4084080 | ~3.49511 |
|
| 19 | 275295799 | /77597520 | ~3.54774 |
|
| 20 | 55835135 | /15519504 | ~3.59774 |
|
| 21 | 18858053 | /5173168 | ~3.64536 |
|
| 22 | 19093197 | /5173168 | ~3.69081 |
|
| 23 | 444316699 | /118982864 | ~3.73429 |
|
| 24 | 1347822955 | /356948592 | ~3.77596 |
|
| 25 | 34052522467 | /8923714800 | ~3.81596 |
|
| 26 | 34395742267 | /8923714800 | ~3.85442 |
|
| 27 | 312536252003 | /80313433200 | ~3.89146 |
|
| 28 | 315404588903 | /80313433200 | ~3.92717 |
|
| 29 | 9227046511387 | /2329089562800 | ~3.96165 |
|
| 30 | 9304682830147 | /2329089562800 | ~3.99499 |
|
Related Series
Alternating Harmonic Series
There's a cousin to the harmonic series called the alternating harmonic series. In this one, you subtract every other term:
Unlike the regular harmonic series, this one actually adds up to a specific number! It equals the natural logarithm of 2, which is about 0.693.
This series is special because if you change the order of the numbers you're adding, the sum can change.
General Harmonic Series
You can also have a general harmonic series which looks a bit different:
Here, 'a' and 'b' are just numbers. Even these general harmonic series still grow forever (diverge), just like the original one.
p-series
A more general type of series is called the p-series:
Here, 'p' is any real number.
- If p = 1, it's our original harmonic series, which diverges (grows forever).
- If p is less than or equal to 1 (like 1/2 or 0.5), the series also diverges.
- But if p is greater than 1 (like 2 or 3), then the series actually adds up to a specific number! For example, when p = 2, the sum is exactly π26, which is about 1.645. This was a famous problem called the Basel problem.
Depleted Harmonic Series
What if you take the harmonic series and remove some terms? For example, imagine you remove every fraction where the number on the bottom (denominator) has the digit '9' in it (like 1/9, 1/19, 1/29, 1/90, etc.).
It might seem like it would still grow forever, but surprisingly, this "depleted" harmonic series actually adds up to a specific number! Its value is less than 80. This is true if you remove any specific digit or string of digits from the denominators.
Applications and Surprises
The harmonic series can lead to some surprising results because it grows forever, even though its terms get tiny. Here are a few examples:
- The Worm on the Rubber Band: Imagine a worm crawling on a super stretchy rubber band. The worm crawls 1 centimeter per minute, and the rubber band stretches 1 meter (100 centimeters) per minute. Will the worm ever reach the end of the 1-meter rubber band?
* It seems impossible, but the answer is yes! The distance the worm covers compared to the total length of the band is related to the harmonic series. Because the harmonic series eventually grows larger than any number, the worm will eventually reach the end. However, it would take an incredibly long time – more than 1037 years!
- The Jeep Problem: This puzzle asks how much fuel a jeep needs to cross a desert if it can only carry a limited amount of fuel and can leave fuel drops along the way.
* The amount of fuel needed to travel a certain distance is connected to the harmonic series. Because the series grows so slowly, the fuel needed increases very, very quickly (exponentially) for longer distances.
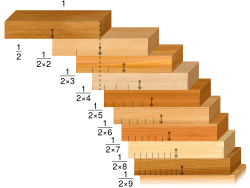
- The Block-Stacking Problem: Can you stack identical dominoes or blocks on the edge of a table so that the top block hangs out as far as you want without falling?
* Yes, you can! If you have enough blocks, you can stack them in a way that the overhang can be as large as you like. The math behind how far they can hang is based on the harmonic series.
- The Swimmer in the Pool: Imagine a swimmer crossing a 10-meter pool. They start at 2 meters per second. Every time they touch a wall, their speed increases by another 2 meters per second.
* In theory, the swimmer's speed could become unlimited. But the time it takes to reach a certain speed depends on the sum of the harmonic series. For example, to reach the speed of light, the swimmer would need to cross the pool 150 million times! But the total time for this would only be about 97 seconds, which is a very short time for so many crossings.
Related pages
- Harmonic progression
- List of sums of reciprocals
- Eric W. Weisstein, Harmonic Series at MathWorld.
- Eric W. Weisstein, Book Stacking Problem at MathWorld.
Images for kids
See also
 In Spanish: Serie armónica (matemática) para niños
In Spanish: Serie armónica (matemática) para niños


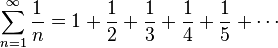
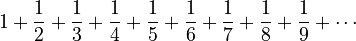
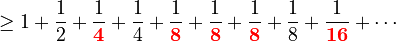
![\begin{align}
&{} 1 + \left(\frac{1}{2}\right) + \left(\frac{1}{4}\!+\!\frac{1}{4}\right) + \left(\frac{1}{8}\!+\!\frac{1}{8}\!+\!\frac{1}{8}\!+\!\frac{1}{8}\right) + \left(\frac{1}{16}\!+\!\cdots\!+\!\frac{1}{16}\right) + \cdots \\[12pt]
={} &1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots = \infty
\end{align}](/images/math/0/4/f/04f24c0f5ba8d31323893c9f60f91e13.png)