Gamma function Facts for Kids

The gamma function (written as Γ(z)) is a special tool in mathematics. Think of it as an extension of the factorial function. You might know factorials from numbers like 5! (which is 5 × 4 × 3 × 2 × 1 = 120). The gamma function helps us calculate factorials for numbers that aren't just positive whole numbers, like fractions or even complex numbers.

The gamma function along part of the real axis

For any positive integer n, the gamma function is related to the factorial like this: Γ(n) = (n-1)!

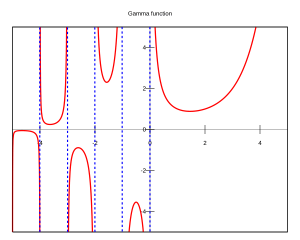
For example, Γ(4) = (4-1)! = 3! = 3 × 2 × 1 = 6. The gamma function is defined for almost all complex numbers. However, it does not work for zero or negative whole numbers. For other numbers, it is defined using a special kind of math problem called an integral.

The symbol Γ(z) was first used by a mathematician named Adrien-Marie Legendre.

What the Gamma Function Does
Special Values
Pi Function
How the Gamma Function is Used
Images for kids
See also

What the Gamma Function Does

The gamma function has some interesting properties that help mathematicians use it. One important rule is called the Euler's reflection formula. It connects the gamma function of a number z with the gamma function of (1 - z).

Another useful rule is the duplication formula. This formula shows how the gamma function of z relates to the gamma function of 2z.

A cool fact is that the gamma function of 1/2 is equal to the square root of pi (π): Γ(1/2) = √π

This value can be found using the reflection or duplication formulas. It also comes from a special type of Gaussian integral when you look at the integral definition of the gamma function.

Special Values

Here are some specific values of the gamma function:

Γ(-3/2) ≈ 2.363
Γ(-1/2) ≈ -3.545
Γ(1/2) = √π ≈ 1.772
Γ(1) = 0! = 1
Γ(3/2) = 1/2√π ≈ 0.886
Γ(2) = 1! = 1
Γ(5/2) = 3/4√π ≈ 1.329
Γ(3) = 2! = 2
Γ(7/2) = 15/8√π ≈ 3.323
Γ(4) = 3! = 6

Pi Function

Another mathematician, Carl Friedrich Gauss, introduced something called the Pi function (written as Π(z)). This is just another way to write the gamma function. It's defined as: Π(z) = Γ(z+1)

This means that for any non-negative whole number n: Π(n) = n!

So, the Pi function directly gives you the factorial of a number.

How the Gamma Function is Used

The gamma function is very important in many areas of mathematics. One key area is analytic number theory. It helps mathematicians study the Riemann zeta function, which is related to prime numbers.

In 1859, a mathematician named Bernhard Riemann found a special connection between the gamma function and the Riemann zeta function. This connection helps us understand more about how prime numbers are spread out.