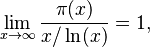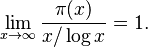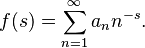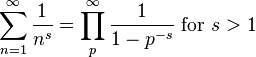Analytic number theory facts for kids

Riemann zeta function ζ(s) in the complex plane. The colors show how the function acts on different numbers. Black means the value is close to zero.

In mathematics, analytic number theory is a special part of number theory. It uses tools from mathematical analysis (like calculus and limits) to solve problems about integers. It helps us understand how numbers behave, especially prime numbers.

This field is often said to have started in 1837. That's when Peter Gustav Lejeune Dirichlet used special functions called Dirichlet L-functions. He used them to prove Dirichlet's theorem on arithmetic progressions. Analytic number theory is famous for its work on prime numbers. This includes the Prime Number Theorem and the Riemann zeta function. It also deals with additive number theory, like the Goldbach conjecture and Waring's problem.

What are the main parts of analytic number theory?
A quick look at history
What problems does analytic number theory solve?
How does analytic number theory work?
- Dirichlet series
- Riemann zeta function
See Also

What are the main parts of analytic number theory?

Analytic number theory has two main parts. They are divided by the types of problems they try to solve.

Multiplicative number theory looks at how prime numbers are spread out. For example, it tries to guess how many primes are in a certain range. Key ideas here are the prime number theorem and Dirichlet's theorem on primes in arithmetic progressions.
Additive number theory focuses on adding integers together. An example is Goldbach's conjecture. This idea says that every even number bigger than 2 is the sum of two prime numbers. A big success in additive number theory was solving Waring's problem.

A quick look at history

Early ideas

Many ideas in analytic number theory came from trying to understand the prime number theorem. Let's say π(x) is a function that counts how many prime numbers are less than or equal to x. For example, π(10) = 4, because 2, 3, 5, and 7 are primes less than or equal to 10.

The prime number theorem says that x / ln(x) is a very good guess for π(x). This means that as x gets very, very big, the count of primes (π(x)) and x / ln(x) become almost the same.

\lim_{x\to\infty}\frac{\pi(x)}{x/\ln(x)}=1,

This is known as the "asymptotic law of distribution of prime numbers."

Adrien-Marie Legendre thought about this in the late 1700s. He guessed a formula to estimate primes. Later, Carl Friedrich Gauss also thought about this problem when he was only 15 or 16 years old. He wrote down a similar idea in his notebook. In 1838, Peter Gustav Lejeune Dirichlet found his own way to estimate primes. All these ideas pointed to the same main result.

Dirichlet's contributions

Johann Peter Gustav Lejeune Dirichlet is seen as the founder of analytic number theory. He made many important discoveries. In 1837, he published Dirichlet's theorem on arithmetic progressions. He used math analysis to solve a problem about numbers. This was a new way of thinking. To prove his theorem, he created Dirichlet characters and L-functions.

Chebyshev's work

In the mid-1800s, the Russian mathematician Pafnuty L'vovich Chebyshev tried to prove the prime number theorem. He used a special function called the zeta function. This was before Riemann's famous work. Chebyshev proved a slightly weaker version of the theorem. He showed that if the prime number theorem's limit exists, it must be 1. He also proved that there is always a prime number between any number n and 2n (for n ≥ 2). This is called Bertrand's postulate.

Riemann's big ideas

Bernhard Riemann made huge contributions to modern analytic number theory. In a short paper in 1859, he looked at the Riemann zeta function. He showed how important it was for understanding how prime numbers are spread out. He made several guesses about this function. One of them is the famous Riemann hypothesis.

Hadamard and de la Vallée-Poussin

Building on Riemann's ideas, two mathematicians proved the prime number theorem independently. They were Jacques Hadamard and Charles Jean de la Vallée-Poussin. Their proofs came out in the same year, 1896. Both used methods from complex analysis. A key part of their proof was showing that the Riemann zeta function is not zero for certain complex numbers.

Modern developments

After 1950, a big change was the growth of sieve methods. These are ways to count things in number theory. They are like puzzles. Another new area is probabilistic number theory. This uses ideas from probability to guess how number functions behave. For example, how many prime numbers divide a certain number.

Recent breakthroughs by mathematicians like Yitang Zhang and James Maynard have used new methods. These methods help us understand the gaps between prime numbers.

Analytic number theory often improves old techniques. This helps to make results more accurate and useful. For example, the circle method is now used in new ways.

What problems does analytic number theory solve?

Analytic number theory usually gives approximate answers. It provides estimates for different number functions. It doesn't give exact answers about the structure of integers.

Multiplicative number theory problems

Euclid showed that there are endless prime numbers. A big question is how these primes are spread out. Gauss guessed that the number of primes less than a large number N is close to a special calculation involving logarithms.

In 1859, Bernhard Riemann used complex analysis and the Riemann zeta function. He found a formula for the number of primes less than x. The main part of his formula was exactly what Gauss had guessed. Riemann also found that errors in this formula are linked to the zeros of the zeta function.

Using Riemann's ideas, Jacques Hadamard and Charles Jean de la Vallée-Poussin proved Gauss's guess. They showed that if π(x) is the number of primes less than or equal to x, then:

\lim_{x \to \infty} \frac{\pi(x)}{x/\log x} = 1.

This amazing result is the prime number theorem. It's a central idea in analytic number theory. It roughly says that for a big number N, the primes less than or equal to N are about N/log(N).

We can also ask about primes in an arithmetic progression. This is a list of numbers like 3, 7, 11, 15... (where you add the same number each time). Dirichlet proved that any such list (with certain rules) has infinitely many primes. The prime number theorem can be used here too.

There are also many unsolved problems. For example, the twin prime conjecture asks if there are endless pairs of primes that are only 2 apart (like 3 and 5, or 11 and 13).

Additive number theory problems

One important problem is Waring's problem. It asks if any positive integer can be written as the sum of a certain number of powers. For example, can any number be written as the sum of a few squares?

For squares (k = 2), Lagrange proved in 1770 that every positive integer is the sum of at most four squares. Hilbert proved the general case in 1909. He used algebraic methods. Later, Hardy and Littlewood used analytic tools. Their "circle method" gives clear upper limits for how many powers are needed.

Diophantine problems

Diophantine problems are about finding integer solutions to equations. For example, the Gauss circle problem asks how many integer points (x, y) are inside or on a circle centered at the origin with radius r.

It's easy to see the answer is close to the circle's area, which is πr². The hard part is figuring out how big the error is. Gauss showed the error is not too big. Later, Sierpiński improved this in 1906. Since then, mathematicians have tried to make the error estimate even smaller.

How does analytic number theory work?

Dirichlet series

One very useful tool in multiplicative number theory is Dirichlet series. These are special functions that look like an endless sum:

f(s)=\sum_{n=1}^\infty a_nn^{-s}.

These series can help us understand how numbers behave when multiplied. When you multiply two Dirichlet series, their coefficients combine in a special way. This allows mathematicians to get information about number functions by studying these series.

Riemann zeta function

Euler showed a cool link between the sum of 1/n^s and prime numbers:

\sum_{n=1}^\infty \frac {1}{n^s} = \prod_p^\infty \frac {1}{1-p^{-s}}\text{ for }s > 1

This product is taken over all prime numbers p. Euler used this idea to prove that there are infinitely many prime numbers. This was the start of using analysis to study integers.

Later, Riemann looked at this function for complex numbers. He showed that it could be extended to almost the entire complex plane. This function is now called the Riemann Zeta function, written as ζ(s).

Analytic number theorists often want to know how accurate their guesses are. For example, how small is the error in the prime number theorem? Riemann's formula for π(x) shows that this error is linked to the zeros of the zeta function. In his 1859 paper, Riemann guessed that all the "non-trivial" zeros of ζ lie on a special line. This famous guess is the Riemann Hypothesis. If it's true, it has many big effects in number theory. For example, it would mean the error in the prime number theorem is very small.

In the early 1900s, G. H. Hardy and Littlewood studied the zeta function. Hardy proved in 1914 that there are infinitely many zeros of the zeta function on that special line.