Riemann hypothesis facts for kids
The Riemann hypothesis is a big question in mathematics. Many smart people think it's one of the hardest and most important unsolved puzzles in pure mathematics. Pure mathematics is about understanding numbers and shapes for their own sake. It's not about using math to build bridges or solve real-world problems. The answer to the Riemann hypothesis is either "yes" or "no."
This question is named after a mathematician named Bernhard Riemann. He lived a long time ago, in the 1800s. The Riemann hypothesis asks something special about a math tool called the Riemann zeta function.
If we can prove the answer is "yes," it would help mathematicians learn more about prime numbers. Prime numbers are numbers like 2, 3, 5, 7, and so on, that can only be divided by 1 and themselves. Knowing more about them is super important! The Riemann hypothesis is so tough that the Clay Mathematics Institute has offered $1,000,000 to the first person who can prove it.
Contents
What is the Riemann Hypothesis?
Understanding the Riemann Zeta Function
The Riemann zeta function is a type of function. In math, a function is like a machine. You put a number into it, and it gives you another number back. The number you put in is called an "input." The number you get back is called a "value."
For the Riemann zeta function, every input gives you a specific value. You usually get a different value for each input. But if you put the same input in again, you'll always get the same value back. Both the input and the value for this function are special numbers called complex numbers. A complex number has two parts.
What are Non-Trivial Roots?
Sometimes, when you put an input into the Riemann zeta function, the value you get back is zero. When this happens, we call that input a root of the function. It's like finding the "answer" that makes the function equal zero.
There are many roots for the Riemann zeta function. Some are easy to find, and some are hard. We call the easy ones "trivial roots." The hard ones are called "non-trivial roots."
The trivial roots are numbers like -2, -4, -6, and so on (negative even numbers). They are easy because there are clear rules that tell us what they are. Bernhard Riemann himself gave us an equation, called "Riemann's functional equation," that helps us understand these trivial roots.
Finding the Tricky Non-Trivial Roots
The non-trivial roots are much harder to find. They don't follow the same simple rules as the trivial ones. Even though they are hard, many non-trivial roots have been discovered.
Remember that complex numbers have two parts? One part is called the "real part." We noticed something interesting about the real part of all the non-trivial roots we've found so far. Every single one of them has a real part that is exactly 1/2. This is a fraction that means "half."
This observation leads us to Riemann's big question, which is the Riemann hypothesis: "Do all the non-trivial roots have a real part of 1/2?" We are still trying to figure out if the answer is "yes" or "no."
What Do We Know About the Hypothesis?
We don't have the final answer to the Riemann hypothesis yet. But we do know some important things that might help. Riemann's special equation (Riemann's functional equation) tells us a bit about the real parts of the non-trivial roots.
It says that the real parts of all non-trivial roots must be close to 1/2. More specifically, it tells us they must be bigger than 0 but smaller than 1. This means they can't be 0, 1, or any number outside that range. But it doesn't say they have to be exactly 1/2.
The group of complex numbers whose real part is between 0 and 1 is called the "critical strip." The Riemann hypothesis asks if all the non-trivial roots are exactly in the middle of this strip, at 1/2.
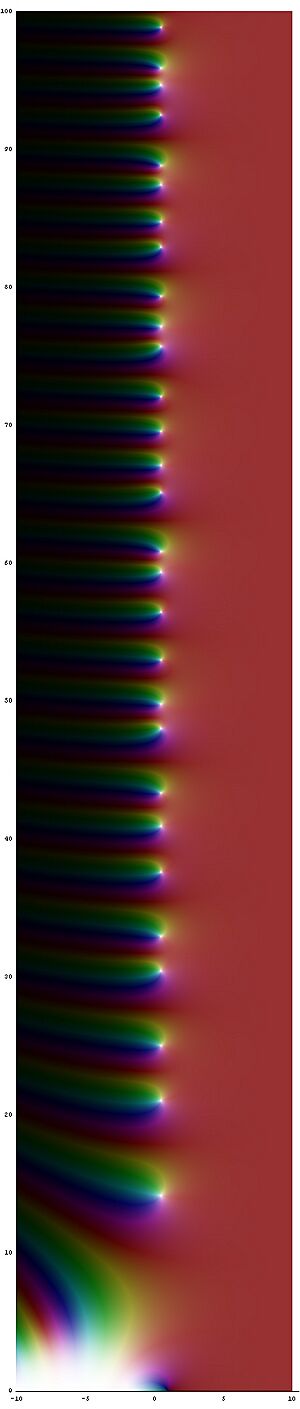
The Riemann Hypothesis in a Picture
Look at the picture at the top of this page. It shows a part of the Riemann zeta function. The white dots in the picture are the non-trivial roots. They all look like they are lined up perfectly down the middle of the picture. Being in the middle means their real part is 1/2. So, all the white dots you see in this picture have a real part of 1/2.
But this picture doesn't show the entire Riemann zeta function because it's too big! So, what about the non-trivial roots that are above or below what the picture shows? Would they also be exactly in the middle? What if some of them break the pattern and are slightly to the left or right of the middle line?
The Riemann hypothesis asks if every single non-trivial root (every white dot, even the ones not shown) would be on that exact middle line. If the answer is "no," it means the "hypothesis is false." That would mean there's at least one white dot that isn't on the 1/2 line.
Images for kids
See also
 In Spanish: Hipótesis de Riemann para niños
In Spanish: Hipótesis de Riemann para niños