Diophantine equation facts for kids

A Diophantine equation is a special kind of equation in mathematics. It's an equation where you are only looking for solutions that are integers (whole numbers like -2, -1, 0, 1, 2, and so on). These equations are named after Diophantus of Alexandria, an ancient Greek mathematician who studied them a long time ago.

Imagine you have an equation like 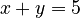Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x + y = 5 . If you're looking for any numbers, you could have 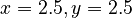Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x=2.5, y=2.5 . But if it's a Diophantine equation, you'd only look for whole numbers, like 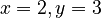Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x=2, y=3 or Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x=1, y=4 .

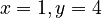Diophantine equations are important because many real-world problems involve only whole numbers. For example, if you're counting people, cars, or pieces of a product, you can't have half a person or a quarter of a car.

What is a Diophantine Equation?

A Diophantine equation is an equation where all the numbers in it (called coefficients) are integers. Also, the equation is usually a polynomial, which means it only involves adding, subtracting, and multiplying variables (like x, y, z) and whole number powers of those variables (like x², y³).

For example, 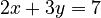Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2x + 3y = 7 is a Diophantine equation if you're looking for integer solutions for x and y. Another example is .

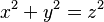Why are they special?

The main thing that makes Diophantine equations special is that we are only interested in integer solutions. This makes them much harder to solve than regular equations where any type of number (like fractions or decimals) is allowed.

Asking Questions About Diophantine Equations

When mathematicians study Diophantine equations, they often ask several key questions:

• Are there any integer solutions at all?
• Are there solutions that are not obvious or easy to find?
• Are there a limited number of solutions, or are there infinitely many?
• Can we find a way (an algorithm) to discover all possible solutions?
• Can we actually calculate a complete list of all solutions in real life?

These questions can be very challenging. Some Diophantine problems have puzzled mathematicians for hundreds of years!

Famous Diophantine Equations

Some Diophantine equations are very well-known in the world of mathematics:

Pythagorean Triples

One of the most famous examples is the equation 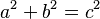. This equation is used in the Pythagorean theorem for right triangles. When we look for integer solutions (whole numbers for a, b, and c), these sets of numbers are called Pythagorean triples.

• The most famous Pythagorean triple is 3, 4, 5 because .
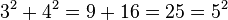• Another example is 5, 12, 13 because Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 5^2 + 12^2 = 25 + 144 = 169 = 13^2 .

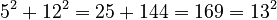There are infinitely many Pythagorean triples!

Fermat's Last Theorem

Another very famous Diophantine equation is related to the Pythagorean triples. It's called Fermat's Last Theorem. The equation is 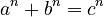Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^n + b^n = c^n .

• For a long time, mathematicians wondered if there were any integer solutions for a, b, and c when 'n' was a whole number greater than 2.
• Pierre de Fermat, a French mathematician from the 1600s, claimed he had a proof that there were no such solutions, but he never wrote it down.
• It took over 350 years for this problem to be finally solved! In 1994, Andrew Wiles, a British mathematician, proved that there are no integer solutions for a, b, and c when 'n' is greater than 2. This was a huge achievement in mathematics.

Pell's Equation

Pell's equation is another type of Diophantine equation that looks like 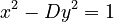Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2 - Dy^2 = 1 , where 'D' is a positive non-square integer. This equation has been studied for centuries and has many interesting properties. It often has infinitely many integer solutions.

Hilbert's Tenth Problem

In 1900, a famous mathematician named David Hilbert presented a list of 23 unsolved problems. His tenth problem was about Diophantine equations. He asked if there could be a general algorithm (a step-by-step method) that could tell us, for *any* given Diophantine equation, whether it has integer solutions or not.

• This problem was finally solved in 1970 by Yuri Matiyasevich, a Russian mathematician.
• The answer was surprising: No such general algorithm exists! This means there's no single computer program or method that can always tell us if a Diophantine equation has integer solutions. Each equation might need a different approach.

Diophantine equations continue to be an exciting area of study for mathematicians today!