Exponent facts for kids
An exponent is a special number that tells you how many times to multiply a number by itself. Think of it as a shortcut for repeated multiplication!
For example, in the number 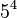 , the number 5 is called the base, and the small number 4 is the exponent. You can read this as "5 to the power of 4". It means you multiply 5 by itself 4 times:
, the number 5 is called the base, and the small number 4 is the exponent. You can read this as "5 to the power of 4". It means you multiply 5 by itself 4 times: 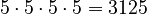 .
.
In general, if you see 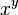 , it means you multiply the base number
, it means you multiply the base number  by itself
by itself  times.
times.
When a number is raised to the power of two, like 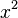 , we often say it's "squared". This is because if you have a square with sides of length
, we often say it's "squared". This is because if you have a square with sides of length  , its area is
, its area is 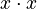 , or
, or 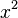 .
.
Similarly, when a number is raised to the power of three, like 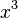 , we say it's "cubed". This is because a cube with sides of length
, we say it's "cubed". This is because a cube with sides of length  has a volume of
has a volume of 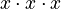 , or
, or 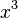 .
.
Exponents are super useful in algebra and other parts of mathematics. They help us write very long multiplication problems in a much shorter way.
Contents
Basic Rules of Exponents
There are a few simple rules that help us work with exponents. Let's look at them!
Product Rule: Multiplying Exponents
When you multiply numbers with the same base, you can add their exponents.
The rule is: 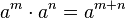
- What it means:* If you have
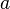 multiplied by itself
multiplied by itself 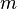 times, and you multiply that by
times, and you multiply that by 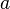 multiplied by itself
multiplied by itself  times, you end up with
times, you end up with 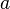 multiplied by itself a total of
multiplied by itself a total of 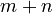 times.
times.
- Example:*
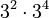 This means
This means 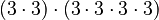 . If you count all the 3s, there are 6 of them. So,
. If you count all the 3s, there are 6 of them. So, 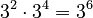 . Notice that
. Notice that 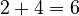 , which matches the rule!
, which matches the rule!
Quotient Rule: Dividing Exponents
When you divide numbers with the same base, you can subtract their exponents.
The rule is: 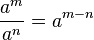
- What it means:* If you have
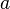 multiplied
multiplied 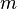 times on top and
times on top and 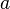 multiplied
multiplied  times on the bottom, you can cancel out
times on the bottom, you can cancel out  of the
of the 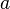 's from both top and bottom. You are left with
's from both top and bottom. You are left with 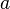 multiplied
multiplied 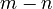 times.
times.
- Example:*
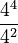 This means
This means 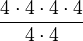 . You can cancel two 4s from the top and two 4s from the bottom. You are left with
. You can cancel two 4s from the top and two 4s from the bottom. You are left with 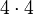 , which is
, which is 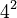 . Notice that
. Notice that 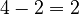 , which matches the rule!
, which matches the rule!
Sometimes, when you subtract the exponents, you might get a negative number. We'll learn about that next!
Zero Rule: Exponent of Zero
Any number (except zero) raised to the power of zero is always 1.
The rule is: 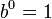 (where
(where 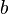 is not zero)
is not zero)
- Why it works:*
Let's use the Quotient Rule. We know that 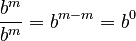 . But we also know that any number divided by itself is 1 (as long as it's not zero). So,
. But we also know that any number divided by itself is 1 (as long as it's not zero). So, 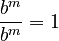 . This means
. This means 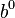 must be equal to 1!
must be equal to 1!
Negative Exponents
A negative exponent means you take the reciprocal of the number with a positive exponent. The reciprocal of a number is 1 divided by that number.
The rule is: 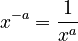
- What it means:* Instead of multiplying, a negative exponent tells you to divide. For example,
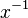 means
means 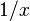 .
.
- Example:*
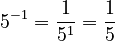
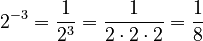
- Why it works:*
Let's think about the Product Rule again: 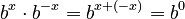 . We already learned that
. We already learned that 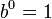 . So,
. So, 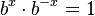 . To find out what
. To find out what 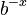 is, we can divide both sides by
is, we can divide both sides by 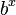 :
: 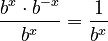 This leaves us with
This leaves us with  .
.
If you have a number multiplied by a term with a negative exponent, like 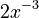 , it means
, it means 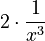 , which is
, which is 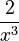 .
.
Related pages
See also
 In Spanish: Potenciación para niños
In Spanish: Potenciación para niños

