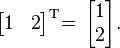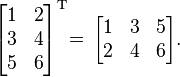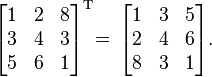Transpose facts for kids

The transpose of a matrix is like flipping it! Imagine you have a grid of numbers (that's a matrix). When you transpose it, you turn all its rows into columns, and all its columns into rows.

Think of it this way: the first row of your original matrix becomes the first column of the new, transposed matrix. The second row becomes the second column, and so on.

We use special symbols to show that a matrix has been transposed. If your matrix is called A, its transpose can be written as A^T, A′, A^tr, or A^t. It's a handy tool in mathematics for solving different kinds of problems!

How to Transpose a Matrix

Let's look at some examples to see how this "flipping" works.

Transposing a Vector

A vector is like a single row or a single column of numbers.

• If you have a row vector like this:

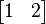When you transpose it, it becomes a column vector:

See how the numbers that were side-by-side are now stacked on top of each other?

Transposing Different Matrices

Here are a few more examples of matrices being transposed:

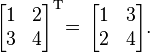
• If you have a 2x2 matrix (2 rows, 2 columns):

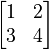Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} Its transpose will swap the numbers across the main diagonal (the line from top-left to bottom-right).

The first row (1, 2) became the first column. The second row (3, 4) became the second column.

• Now, let's try a 3x2 matrix (3 rows, 2 columns):

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} When transposed, it becomes a 2x3 matrix (2 rows, 3 columns):

Notice how the first row (1, 2) is now the first column. The second row (3, 4) is the second column, and the third row (5, 6) is the third column.

• Finally, a 3x3 matrix (3 rows, 3 columns):

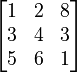Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 & 2 & 8 \\ 3 & 4 & 3 \\ 5 & 6 & 1 \end{bmatrix} Its transpose will also be a 3x3 matrix:

The rows became columns, and the columns became rows.

Properties of Transpose

The transpose operation has some cool rules, called properties, that always work when you're dealing with matrices. If you have two matrices, A and B, these rules are true:

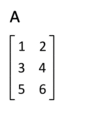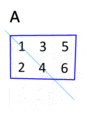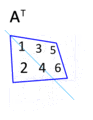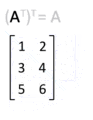
• If you transpose a matrix, and then transpose it again, you get back the original matrix!
• If you multiply two matrices (like A times B) and then transpose the result, it's the same as transposing each matrix first and then multiplying them in reverse order (B^T times A^T).

These properties are very useful in higher-level algebra and computer science.

Related pages

• Invertible matrix

Images for kids

• 

  The transpose A^T of a matrix A can be found by reflecting the numbers across its main diagonal. If you transpose it again, you get the original matrix back!

See also

In Spanish: Matriz transpuesta para niños