Invertible matrix facts for kids
An invertible matrix is a special kind of matrix that has a "partner" matrix. When you multiply a matrix by its partner, you get a special matrix called the identity matrix. Think of it like how multiplying a number by its inverse (like 2 and 1/2) gives you 1.
Contents
What is a Matrix?
A matrix is like a grid or a table filled with numbers. We use matrices to organize data and solve math problems. They are super useful in many areas, from computer graphics to engineering.
For example, a simple matrix might look like this: 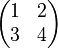Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}
The Identity Matrix
The identity matrix is a very special matrix. It's like the number 1 in regular multiplication. When you multiply any matrix by the identity matrix, the original matrix doesn't change.
The identity matrix has ones along its main diagonal (from top-left to bottom-right) and zeros everywhere else. For a 2x2 matrix, the identity matrix looks like this: 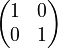Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} We often use the letter 
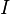to stand for the identity matrix.
Finding the Inverse Matrix
If you have a matrix, let's call it 
, and you can find another matrix, let's call it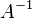 
(read as "A inverse"), such that when you multiply them, you get the identity matrix 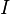, then is an invertible matrix.
The math looks like this: 
And also: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A^{-1} \cdot A = I
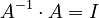
Not all matrices have an inverse. Only special ones do!
How Do We Find It?
Finding the inverse of a matrix can be a bit tricky, especially for big matrices. There are step-by-step methods, called algorithms, to calculate it. One common method is called Gaussian elimination.
It can take a lot of computer power to find the inverse of very large matrices. This is why mathematicians and computer scientists look for faster ways to do it.
Why Are Invertible Matrices Important?
Invertible matrices are used a lot in computer graphics. For example, when you play a video game or watch an animated movie, matrices help move objects around on the screen. An inverse matrix can help "undo" a movement or transformation.
They are also used in cryptography (making and breaking codes) and in solving systems of equations in science and engineering.
Related pages
See also
In Spanish: Matriz invertible para niños
