Gaussian elimination Facts for Kids

Gaussian elimination, also known as row reduction, is a clever method used in mathematics to solve groups of linear equations. Think of it like a puzzle where you have several equations with unknown values (like x, y, z), and you need to find what those values are.

This method is named after Carl Friedrich Gauss, a very famous German mathematician. Even though the method is named after him, he didn't actually invent it. He just wrote a lot about it and helped make it well-known.

To use Gaussian elimination, you first take the numbers from your equations and put them into a special grid called an augmented matrix. This matrix helps you organize the numbers. Then, you use simple steps called elementary row operations to make the matrix simpler. There are three main types of these operations:

Type 1: You can swap any two rows in the matrix.
Type 2: You can multiply an entire row by any number, as long as it's not zero.
Type 3: You can add or subtract one row from another row.

The main goal of Gaussian elimination is to change the matrix into a special look called row-echelon form. When a matrix is in row-echelon form, each row starts with more zeros than the row above it, when you read from left to right.

Sometimes, people take it a step further to get to reduced row-echelon form. This means the matrix is in row-echelon form, and the only non-zero number in each row is a '1'. When you do this extra step, it's sometimes called Gauss-Jordan elimination.

How to Solve Equations with Gaussian Elimination
See also

How to Solve Equations with Gaussian Elimination

Let's look at an example to see how Gaussian elimination works. Imagine you have these three equations and you want to find the values for x, y, and z:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} 2x &&\; + \;&& y &&\; - \;&& z &&\; = \;&& 8 & \\ -3x &&\; - \;&& y &&\; + \;&& 2z &&\; = \;&& -11 & \\ -2x &&\; + \;&& y &&\; +\;&& 2z &&\; = \;&& -3 & \end{alignat}

Step 1: Create the Augmented Matrix

First, we turn these equations into an augmented matrix. Each equation becomes a row in the matrix. The numbers in front of x, y, and z (called coefficients) go on one side. The numbers on the right side of the equals sign go on the other side. For our equations, the augmented matrix looks like this:

\left[ \begin{array}{ccc|c} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \end{array} \right]

Step 2: Use Row Operations to Simplify

Now, we use the row operations to simplify the matrix. The goal is to get zeros in certain places. The table below shows how we change both the equations and the matrix at the same time.

System of equations	Row operations	Augmented matrix
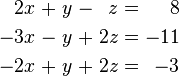Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} 2x &&\; + \;&& y &&\; - \;&& z &&\; = \;&& 8 & \\ -3x &&\; - \;&& y &&\; + \;&& 2z &&\; = \;&& -11 & \\ -2x &&\; + \;&& y &&\; +\;&& 2z &&\; = \;&& -3 & \end{alignat}		$\left[ \begin{array}{ccc\|c} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \end{array} \right]$
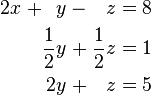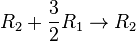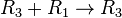Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} 2x &&\; + && y &&\; - &&\; z &&\; = \;&& 8 & \\ && && \frac{1}{2}y &&\; + &&\; \frac{1}{2}z &&\; = \;&& 1 & \\ && && 2y &&\; + &&\; z &&\; = \;&& 5 & \end{alignat}	$R_2 + \frac{3}{2}R_1 \rightarrow R_2$ $R_3 + R_1 \rightarrow R_3$	$\left[ \begin{array}{ccc\|c} 2 & 1 & -1 & 8 \\ 0 & 1/2 & 1/2 & 1 \\ 0 & 2 & 1 & 5 \end{array} \right]$
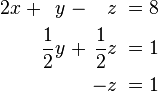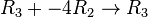Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} 2x &&\; + && y \;&& - &&\; z \;&& = \;&& 8 & \\ && && \frac{1}{2}y \;&& + &&\; \frac{1}{2}z \;&& = \;&& 1 & \\ && && && &&\; -z \;&&\; = \;&& 1 & \end{alignat}	$R_3 + -4R_2 \rightarrow R_3$	$\left[ \begin{array}{ccc\|c} 2 & 1 & -1 & 8 \\ 0 & 1/2 & 1/2 & 1 \\ 0 & 0 & -1 & 1 \end{array} \right]$

At this point, the matrix is in row-echelon form. This is also sometimes called triangular form because the non-zero numbers form a triangle.

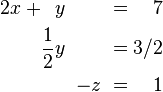
Step 3: Get to Reduced Row-Echelon Form (Gauss-Jordan)

To find the exact answers for x, y, and z, we continue simplifying the matrix until it's in reduced row-echelon form.

System of equations	Row operations	Augmented matrix
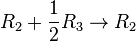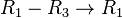Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} 2x &&\; + && y \;&& &&\; \;&& = \;&& 7 & \\ && && \frac{1}{2}y \;&& &&\; \;&& = \;&& 3/2 & \\ && && && &&\; -z \;&&\; = \;&& 1 & \end{alignat}	$R_2+\frac{1}{2}R_3 \rightarrow R_2$ $R_1 - R_3 \rightarrow R_1$	$\left[ \begin{array}{ccc\|c} 2 & 1 & 0 & 7 \\ 0 & 1/2 & 0 & 3/2 \\ 0 & 0 & -1 & 1 \end{array} \right]$
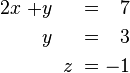Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} 2x &&\; + && y \;&& &&\; \;&& = \;&& 7 & \\ && && y \;&& &&\; \;&& = \;&& 3 & \\ && && && &&\; z \;&&\; = \;&& -1 & \end{alignat}	$2R_2 \rightarrow R_2$ $-R_3 \rightarrow R_3$	$\left[ \begin{array}{ccc\|c} 2 & 1 & 0 & 7 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{array} \right]$
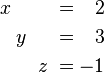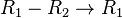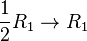Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{alignat}{7} x &&\; && \;&& &&\; \;&& = \;&& 2 & \\ && && y \;&& &&\; \;&& = \;&& 3 & \\ && && && &&\; z \;&&\; = \;&& -1 & \end{alignat}	$R_1 - R_2 \rightarrow R_1$ $\frac{1}{2}R_1 \rightarrow R_1$	$\left[ \begin{array}{ccc\|c} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{array} \right]$

Now the matrix is in reduced row-echelon form! This final matrix directly tells us the answers: x = 2, y = 3, and z = -1. This is how Gaussian elimination helps us solve complex systems of equations step-by-step.

Gaussian elimination facts for kids

Contents

How to Solve Equations with Gaussian Elimination

Step 1: Create the Augmented Matrix

Step 2: Use Row Operations to Simplify

Step 3: Get to Reduced Row-Echelon Form (Gauss-Jordan)

See also