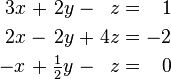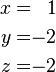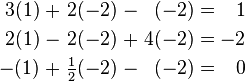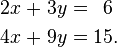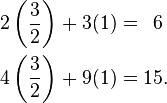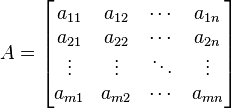System of linear equations Facts for Kids

Imagine three flat surfaces (planes) meeting at one point. That point is the solution to a system of three linear equations!

In mathematics, a system of linear equations is like a puzzle with several math problems that all need to be true at the same time. It's a group of linear equations that all use the same set of variables.

What is a System of Linear Equations?
A Simple Example
Using Matrices to Solve
Finding Solutions to Linear Systems
Everyday Uses
- Online Tools
Related Topics
See also

What is a System of Linear Equations?

Mathematicians use equations to show how different things are connected. A "linear equation" means that the variables (like x or y) appear only once in each equation. They are not raised to a power (like x²).

A "system" of linear equations means you have several of these equations. The goal is to find numbers for each variable that make all the equations true at the same time. If you can't find any numbers that work for every equation, the system is called "inconsistent."

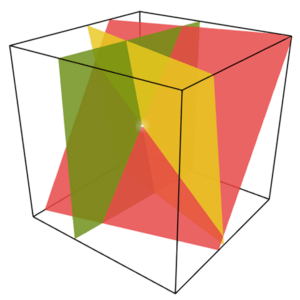
For example, look at this system with three equations and three variables (x, y, z):

\begin{alignat}{7} 3x &&\; + \;&& 2y &&\; - \;&& z &&\; = \;&& 1 & \\ 2x &&\; - \;&& 2y &&\; + \;&& 4z &&\; = \;&& -2 & \\ -x &&\; + \;&& \tfrac{1}{2} y &&\; - \;&& z &&\; = \;&& 0 & \end{alignat}

A "solution" is when you find numbers for x, y, and z that make all three equations correct. For the system above, the solution is:

\begin{alignat}{2} x & = & 1 \\ y & = & -2 \\ z & = & -2 \end{alignat}

Let's check if it works:

\begin{alignat}{7} 3(1) &&\; + \;&& 2(-2) &&\; - \;&& (-2) &&\; = \;&& 1 & \\ 2(1) &&\; - \;&& 2(-2) &&\; + \;&& 4(-2) &&\; = \;&& -2 & \\ -(1) &&\; + \;&& \tfrac{1}{2} (-2) &&\; - \;&& (-2) &&\; = \;&& 0 & \end{alignat}

All three equations are true!

Understanding linear systems is a big part of linear algebra. This is a key area in modern mathematics. Computers use special algorithms to find solutions. These methods are very important in many fields, like engineering, physics, chemistry, computer science, and economics.

Sometimes, a very complex system (called a non-linear system) can be simplified. We can make it look like a linear system. This is a helpful trick when creating a mathematical model or a computer simulation. For really complex systems, there might be many equations and many variables. Often, the number of equations and variables is the same. Sometimes, there are more variables than equations. In that case, the solution might be a range of values, not just one exact answer.

A Simple Example

Let's look at the easiest type of linear system. It has two equations and two variables (x and y):

\begin{alignat}{5} 2x &&\; + \;&& 3y &&\; = \;&& 6 & \\ 4x &&\; + \;&& 9y &&\; = \;&& 15&. \end{alignat}

Here's one way to solve it:

First, take the top equation and figure out what x equals in terms of y:

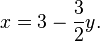
: $x = 3 - \frac{3}{2}y.$

Now, put this new expression for x into the bottom equation:

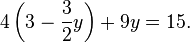
: $4\left( 3 - \frac{3}{2}y \right) + 9y = 15.$

This equation now only has the variable y. If you solve it, you'll find that $y = 1$ .
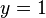Finally, put 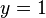$y = 1$ back into the equation for x. You'll get $x = 3/2$ .

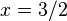Let's check our answers:

\begin{alignat}{5} 2\left(\frac{3}{2}\right) &&\; + \;&& 3(1) &&\; = \;&& 6 & \\ 4\left(\frac{3}{2}\right) &&\; + \;&& 9(1) &&\; = \;&& 15&. \end{alignat}

Both equations are true! This method can be used for systems with more variables too.

Using Matrices to Solve

Often, all the numbers in front of the variables (called coefficients) are put into a special grid called a matrix. This is called a coefficient matrix.

A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}

The variables and the answers can also be written as special lists called vectors:

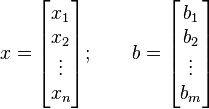x = \begin{bmatrix} x_1\\ x_2 \\ \vdots \\ x_n\end{bmatrix};\qquad b = \begin{bmatrix} b_1\\ b_2 \\ \vdots \\ b_m\end{bmatrix}

This allows us to write the whole system in a very short way:

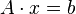A \cdot x = b

This makes it easier for computers to solve many equations at once.

Finding Solutions to Linear Systems

When you try to solve a system of linear equations, there are three possible outcomes:

No solution: The equations contradict each other.
Exactly one solution: There is only one set of numbers that makes all equations true.
Many solutions: There are lots of different sets of numbers that work. Often, this means there are an infinite number of solutions.

There are two main types of methods for solving these systems:

Direct methods: These methods find the solution in a fixed number of steps.

* One way is to solve for one variable in terms of others. Then you replace that variable in other equations. You keep doing this until you find the values for all variables. * Another way is to change two equations so that one side is the same for both. Then you can combine them into a new, simpler equation. * Other direct methods include Gaussian elimination, QR decomposition, Cholesky decomposition, and Cramer's rule.

Iterative methods: These methods use many steps to get closer and closer to the right answer. They are like making better and better guesses.

* Examples include Relaxation (like the Gauss-Seidel and Jacobi methods), Multigrid method, and Krylow method.

Sometimes, you have many more measurements than unknowns. For example, in geodesy (the science of measuring the Earth), you might have many slightly inaccurate measurements. In these cases, there's usually no perfect solution. Methods like Least squares can find the "best fit" solution. This solution is often used as if it were the exact one.

Computers can solve systems of equations very quickly. The fastest known method was developed in 1990 by Don Coppersmith and Shmuel Winograd.

Everyday Uses

Computers solve systems of linear equations all the time!

They are used in weather forecasting models to predict the weather.
Factories that make things like Hot dogs use them. They can quickly adjust recipes when the prices of ingredients change.
College cafeterias use them to figure out how much food to cook. They look at past data to see how much students ate when given different choices.

Online Tools

You can try an online linear solver to see how it works.

System of linear equations facts for kids

Contents