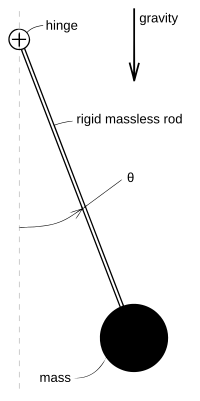Nonlinear system facts for kids

Imagine a system where a small change at the start can lead to a huge, unexpected difference at the end. That's often how a nonlinear system works! In mathematics and science, a nonlinear system is one where the output doesn't change directly in proportion to the input.

Think of it like this: If you push a swing a little harder (a linear system), it goes a little higher. But in a nonlinear system, pushing it a little harder might make it swing wildly, or even flip over!

Scientists and engineers are very interested in nonlinear systems because most things in the real world are nonlinear. This includes everything from how weather patterns form to how populations of animals change over time. Unlike simpler linear systems, nonlinear systems can sometimes seem chaotic, hard to predict, or even surprising.

When we describe these systems using math, we often use a nonlinear system of equations. These are sets of equations where the unknown values are part of more complex math expressions, not just simple additions or multiplications. Because these equations are tough to solve exactly, scientists often use simpler, "linear" versions to get an idea of what's happening. However, this simplification can hide some really cool and complex behaviors, like solitons (special waves) or true chaos. That's why understanding nonlinear systems is so important!

Some people even call the study of these systems "nonlinear science." But as the famous mathematician Stanisław Ulam once joked, calling it "nonlinear science" is "like referring to the bulk of zoology as the study of non-elephant animals." It just shows how common and important nonlinear systems are!

What Makes a System Nonlinear?

In math, a "linear" relationship is very straightforward. If you have a function, let's call it f(x), it's linear if it follows two simple rules:

• Adding things up: If you add two inputs, say x and y, and then put them into the function, the result is the same as putting x in, putting y in, and then adding their results. So, f(x + y) = f(x) + f(y).
• Scaling things: If you multiply your input x by a number, say α, and then put it into the function, the result is the same as putting x in first and then multiplying its result by α. So, f(αx) = αf(x).

If a system or an equation doesn't follow these two rules, then it's nonlinear. Most real-world systems are nonlinear because they don't behave in such simple, predictable ways.

Nonlinear Equations in Algebra

You might have already seen nonlinear equations in your math classes! For example, an equation like: 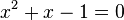Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2 + x - 1 = 0 This is a nonlinear algebraic equation because it has an x squared term. If it only had x to the power of one (like x + 1 = 0), it would be linear.

Finding the solutions (the values of x that make the equation true) for a single nonlinear equation can be done using special methods. But when you have a whole group of these equations that need to be solved at the same time, it gets much harder! This area of study is part of algebraic geometry, a very advanced part of mathematics.

Nonlinear Patterns Over Time

Sometimes, we look at how things change step-by-step or over time. A recurrence relation describes how the next number in a sequence is found from the previous ones. If this relationship is nonlinear, it can lead to very interesting patterns.

A famous example is the logistic map, which shows how a population might grow or shrink over generations. Even with a simple rule, the behavior can become very complex and unpredictable, showing signs of chaos.

Nonlinear Differential Equations

Many real-world systems involve things that change continuously, like the flow of water or the movement of planets. These changes are often described by differential equations. If these equations are not linear, they are called nonlinear differential equations.

One big challenge with nonlinear equations is that you usually can't just combine simple solutions to create more complex ones. In linear systems, if you have two ways something can happen, you can often just add them together to see what happens if both occur. This isn't true for nonlinear systems.

For example, the Navier–Stokes equations describe how fluids (like water or air) move. These are very complex nonlinear equations, which is why predicting weather or designing airplanes is so challenging!

Understanding the Pendulum's Swing

Illustration of a pendulum

A classic example of a nonlinear system is a simple pendulum swinging back and forth. If there's no friction, its motion can be described by a nonlinear equation.

The equation for a pendulum involves the sine of its angle. Because the sine function is nonlinear, the pendulum's motion is also nonlinear.

To make it easier to understand, scientists often use a trick called "linearization." This means they simplify the nonlinear part of the equation to a linear one, but only for a small range of motion.

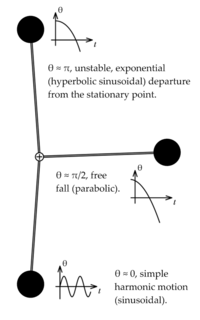
For example, if the pendulum only swings a tiny bit (a "small angle"), the sine of the angle is almost the same as the angle itself. So, the equation becomes much simpler and describes a simple harmonic oscillator – a smooth, regular back-and-forth motion.

Linearizations of a pendulum

However, if the pendulum swings very wide, or if you try to balance it straight up (which is an unstable position!), the simple linear approximation doesn't work anymore. The full nonlinear equation is needed to truly understand its complex behavior. By looking at different simplified "linear" versions, we can get a good overall picture of how the pendulum behaves in different situations.

Cool Nonlinear Behaviors

Nonlinear systems can show some fascinating and sometimes surprising behaviors:

• Amplitude death: Sometimes, oscillations (like a swinging pendulum) can completely stop because of how they interact with other parts of the system or even with themselves.
• Chaos: This is when a system's future values are impossible to predict far ahead, even though the system follows strict rules. Small changes at the start can lead to huge, unpredictable differences later on. Think of the "butterfly effect" in weather!
• Multistability: A system can have two or more stable states it can settle into. Which state it ends up in depends on its starting conditions.
• Solitons: These are special, self-reinforcing waves that can travel long distances without losing their shape or energy. They're like perfect, stable waves.
• Limit cycles: These are stable, repeating patterns that a system will eventually fall into, even if it starts somewhere else.
• Self-oscillations: These are oscillations that happen automatically in a system because of its internal feedback loops, without any external push.

Examples of Nonlinear Equations

See also

In Spanish: Sistema no lineal para niños