Eigenvalues and eigenvectors Facts for Kids

Illustration of a transformation (of Mona Lisa): This picture shows how an image can be changed. The red arrow (vector) keeps its direction, but the blue one changes. So, the red arrow is an eigenvector for this change. Since it also keeps its length, its eigenvalue is 1.

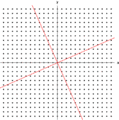
In linear algebra, we look at special ways to change things, called transformations. An eigenvector is like a special arrow (a vector) that doesn't change its direction when you apply one of these transformations. It might get longer or shorter, or even disappear.

The eigenvalue is a number that tells you how much the eigenvector stretches or shrinks. We often use the symbol $\lambda$ for it. The word "eigen" comes from German and means "own" or "typical."

What are Eigenvectors and Eigenvalues?
An Example to Understand
Related pages
Images for kids
See also

What are Eigenvectors and Eigenvalues?

Imagine you have a special grid or a picture. When you apply a mathematical "transformation" to it, like stretching or rotating, most points and arrows on it will change their direction.

But some special arrows, called eigenvectors, will only stretch or shrink. They will still point in the same direction as before. The eigenvalue tells you exactly how much that arrow stretched or shrunk.

The Basic Idea

Let's think about a special kind of mathematical tool called a square matrix, which we can call A. This matrix is like a set of instructions for a transformation.

If you multiply this matrix A by a special arrow (a non-zero vector called v), and the result is just the same arrow v multiplied by a simple number (a scalar called λ), then:

λ is the eigenvalue.
v is the eigenvector.

It looks like this: 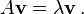$A\mathbf{v} = \lambda \mathbf{v} \, .$

This means the transformation A on vector v does the same thing as just scaling v by the number λ.

Eigenspace: A Family of Eigenvectors

An eigenspace is a group of all eigenvectors that share the same eigenvalue. It also includes the zero vector, even though the zero vector itself is not considered an eigenvector. Think of it as a special line or plane where all arrows on it behave the same way under a transformation.

Beyond Simple Arrows

The ideas of eigenvectors and eigenvalues are used in many areas. Sometimes, the "vectors" aren't just simple arrows. They can be:

Functions
Frequencies
Other complex mathematical objects

Even in these cases, if a "direction" (in a more abstract sense) stays the same after a transformation, we still use the "eigen" prefix. You might hear terms like:

Eigenfunction
Eigenmode
Eigenface
Eigenstate
Eigenfrequency

Eigenvalues and eigenvectors are very important in both pure and applied mathematics. They are used in:

Quantum mechanics (how tiny particles behave)
Facial recognition systems (how computers recognize faces)
Many other scientific and engineering fields

An Example to Understand

Let's look at a simple example with a matrix A: 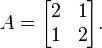$A = \begin{bmatrix} 2 & 1\\1 & 2 \end{bmatrix}.$

Now, let's try a vector x: $\mathbf x = \begin{bmatrix} 3 \\ -3 \end{bmatrix}$

If we multiply A by x, we get: 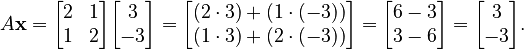Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A \mathbf x = \begin{bmatrix} 2 & 1\\1 & 2 \end{bmatrix} \begin{bmatrix} 3 \\ -3 \end{bmatrix} = \begin{bmatrix} (2 \cdot 3) + (1 \cdot (-3)) \\ (1 \cdot 3) + (2 \cdot (-3)) \end{bmatrix} = \begin{bmatrix} 6 - 3 \\ 3 - 6 \end{bmatrix} = \begin{bmatrix} 3 \\ -3 \end{bmatrix}.

Notice that the result is exactly the same as our original vector x. This means the vector x did not change its direction or length. So, x is an eigenvector, and its eigenvalue is 1 (because 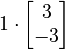Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot \begin{bmatrix} 3 \\ -3 \end{bmatrix} is the same as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 3 \\ -3 \end{bmatrix} ).

Now, let's try a different vector x: 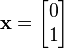$\mathbf x = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$

If we multiply A by this x, we get: 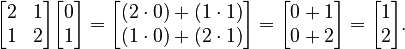Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 2 & 1\\1 & 2 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} (2 \cdot 0) + (1 \cdot 1) \\ (1 \cdot 0) + (2 \cdot 1) \end{bmatrix} = \begin{bmatrix} 0 + 1 \\ 0 + 2 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}.

The result 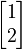Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{bmatrix} 1 \\ 2 \end{bmatrix} is not a simple multiple of the original vector $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ . This means the vector changed its direction. So, this vector is not an eigenvector for matrix A.

Images for kids

In this shear mapping the red arrow changes direction, but the blue arrow does not. The blue arrow is an eigenvector of this shear mapping because it does not change direction, and since its length is unchanged, its eigenvalue is 1.
A 2×2 real and symmetric matrix representing a stretching and shearing of the plane. The eigenvectors of the matrix (red lines) are the two special directions such that every point on them will just slide on them.
An extended version, showing all four quadrants]].
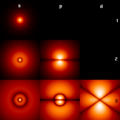
The wavefunctions for an electron in a hydrogen atom are like eigenvectors. They are linked to the electron's energy and angular momentum. The bright areas show where the electron is most likely to be found. The center of each picture is the atomic nucleus.
Eigenfaces are examples of eigenvectors used in facial recognition.