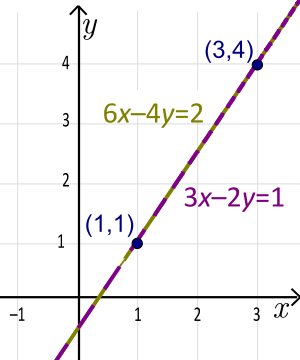Linear function facts for kids

This picture shows a general straight line. It's slanted, meaning its slope isn't zero.

In math, a linear function is a special kind of rule. When you draw its graph, it always makes a straight line. For example, the rule y = 2x - 1 is a linear function. If you pick numbers for x and find y, then plot those points, they will all form a straight line.

What is a Linear Function?

A linear function takes a number as input and gives you another number as output.

• You put a real number (let's call it x) into the function. This x is the input.
• The function then gives you a real number (let's call it y) as the output.
• When you plot all these pairs of numbers (x,y) on a graph, they always make a straight line.

There are three main ways to write linear functions: slope-intercept form, standard form, and parametric form.

This graph shows a line in slope-intercept form. Each line has a unique slope and y-intercept.

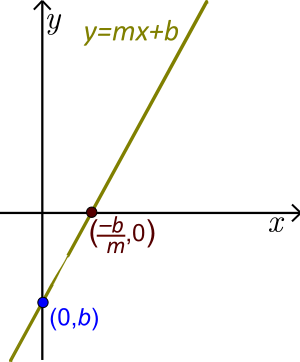
Slope-Intercept Form

The slope-intercept form is a common way to write a linear function. It looks like this: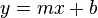

In this form:

• x and y are variables.
  • x is the independent variable. You can choose any real number for x.
  • y is the dependent variable. Its value depends on what you chose for x.
• m and b are constants. They are specific numbers for each line.
  • m is the slope of the line. It tells you how steep the line is and which way it goes (up or down).
  • b is the y-intercept. This is the point where the line crosses the y-axis. It's always the point (0, b).

Understanding Slope (m)

The slope m tells you two things about the line:

• Direction:
  • If m is a positive number (like 2 or 5), the line goes up as you move from left to right.
  • If m is a negative number (like -2 or -5), the line goes down as you move from left to right.
• Steepness:
  • If the number m (ignoring its sign) is small (like 0.5), the line is gentle.
  • If the number m (ignoring its sign) is large (like 5 or -5), the line is steep.

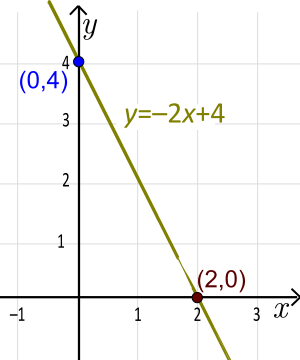
For example, in y = -2x + 4:

• The slope m is -2. This means the line goes down.
• The y-intercept b is 4. So the line crosses the y-axis at (0,4).
• Since the slope is -2, for every 1 step you move to the right on the graph, the line goes down 2 steps.

Horizontal and Vertical Lines

• Horizontal lines are included in linear functions. If m = 0, the equation becomes y = b. This means y is always the same number, no matter what x is. This makes a flat, horizontal line.
• Vertical lines are NOT linear functions. A vertical line has an equation like x = b. It doesn't pass the "vertical line test" (meaning one x value has many y values), so it's not a function.

Graphing a Linear Function

To draw a linear function, you only need two points. 1. Pick two different numbers for x. 2. Use the function rule to find the y value for each x. 3. Plot these two (x,y) points on your graph. 4. Draw a straight line through these two points, extending it in both directions.

Example: Let's graph y = -2x + 4.

• If x = 0, then y = -2(0) + 4 = 4. So, one point is (0,4). (This is the y-intercept!)
• If x = 1, then y = -2(1) + 4 = 2. So, another point is (1,2).
• Plot (0,4) and (1,2) and draw a line through them.

This graph shows a line in standard form. The unique slope-intercept form for this line is y = 1.5x - 0.5.

Standard Form

Another way to write a linear function is the standard form: 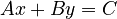Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Ax+By=C In this form:

• x and y are the variables.
• A, B, and C are constants (numbers).
• Important: B cannot be zero. If B were zero, you'd have Ax = C, which is a vertical line (and not a function).

Example: The equation 3x - 2y = 1 is in standard form. Here, A = 3, B = -2, and C = 1.

Sometimes, you might see this form written as 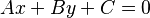. For example, 3x - 2y - 1 = 0 is the same as 3x - 2y = 1.

One thing to know about standard form is that the numbers A, B, and C are not unique. You can multiply all three by the same number, and it will still be the same line. Example: The lines 3x - 2y = 1 and 6x - 4y = 2 are actually the same line! We just multiplied the first equation by 2 to get the second one. If you solve both for y, you'll get y = 1.5x - 0.5.

Linear Function vs. Linear Equation

People sometimes get "linear function" and "linear equation" mixed up.

• A linear equation means that all the variables in it have a power of 1 (like x or y, not x² or y³). A linear equation can have one, two, three, or even more variables.
• A linear function is a special type of linear equation that has exactly two variables (usually x and y), and its graph is a straight line.

* A linear equation with one variable (like x = 5) is just a single point on a number line. * A linear equation with three variables (like x + y + z = 10) makes a flat surface called a plane in 3D space.

Different Ways to Write It

Different countries and subjects might use slightly different letters for linear functions:

• In many places, you'll see 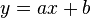, where a is the slope and b is the y-intercept.
• In business or economics, it's sometimes written as , where a is the y-intercept and b is the slope.

Images for kids

• 

  This image shows a line in vector-parametric form. The unique slope-intercept form for this line is y = 1.5x + 2.5.

Related pages

• Line
• Polynomial
• Constant function
• Quadratic equation
• Linear equation