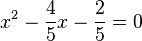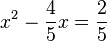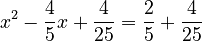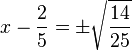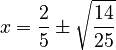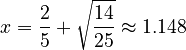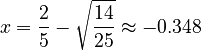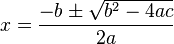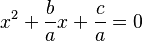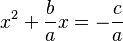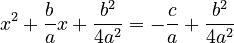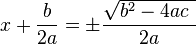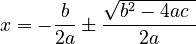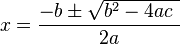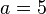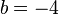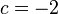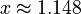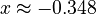Quadratic equation facts for kids
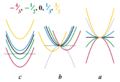
A quadratic equation is a special kind of equation that looks like this: 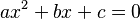 . In this equation, 'a' cannot be zero. When you graph a quadratic equation, it always makes a "U" shape called a parabola on a coordinate plane.
. In this equation, 'a' cannot be zero. When you graph a quadratic equation, it always makes a "U" shape called a parabola on a coordinate plane.
When people work with quadratic equations, they often want to solve them. Solving means finding the points where the graph of the equation crosses the x-axis (the horizontal line). These points are also called the "zeros" or "roots" of the equation. Basically, you are trying to find the value of 'x' that makes the whole equation 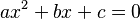 true. The numbers 'a', 'b', and 'c' are called coefficients, and they are all real numbers.
true. The numbers 'a', 'b', and 'c' are called coefficients, and they are all real numbers.
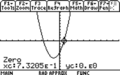
There are different ways to find the value of 'x'. One way is to graph the function. In the picture on the right, the graph crosses the x-axis at 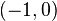 and
and 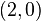 . Graphing makes it easy to see the roots, but it's not always the most convenient way. Luckily, there are other math methods to solve them!
. Graphing makes it easy to see the roots, but it's not always the most convenient way. Luckily, there are other math methods to solve them!
Contents
Factoring quadratic equations
Some quadratic equations can be solved by factoring. Let's look at an example: 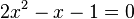 . This equation can be rewritten as
. This equation can be rewritten as 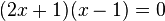 .
.
When two things are multiplied together and the result is zero, it means at least one of them must be zero. So, we get two simpler equations: 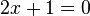 and
and 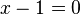 .
.
Now, it's easy to use algebra to find 'x' for each.
- From
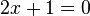 , we get
, we get 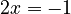 , so
, so 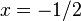 .
. - From
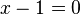 , we get
, we get 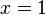 .
.
These two values of 'x' ( -1/2 and 1) are the roots. They make the original quadratic equation equal to zero. This means the graph crosses the x-axis at 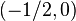 and
and 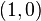 .
.
Completing the square
Not all quadratic equations can be factored easily. For example, 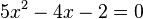 is harder to factor. One way to solve these is called completing the square. This method helps us rewrite the equation so we can easily find 'x'.
is harder to factor. One way to solve these is called completing the square. This method helps us rewrite the equation so we can easily find 'x'.
Here are the steps to solve a quadratic equation by completing the square:
- Step 1: Divide the entire equation by the value of 'a'. In our example, 'a' is 5.
- Step 2: Move the number term (the one without 'x') to the other side of the equation.
- Step 3: "Complete the square" on the left side. To do this, add
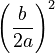 to both sides. In our example, 'b' is -4/5 (from the
to both sides. In our example, 'b' is -4/5 (from the 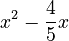 part, where 'a' is now 1). So, we add
part, where 'a' is now 1). So, we add 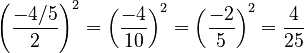 to both sides.
to both sides.
- The left side can now be written as a perfect square:
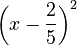 .
. - The right side simplifies to
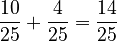 .
.
- So, we have:
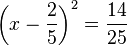
- So, we have:
- Step 4: Find the square root of both sides. Remember to include both positive and negative roots (
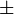 ).
).
- Step 5: Finally, move the number term (
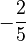 ) to the other side to find 'x'.
) to the other side to find 'x'.
This gives us two values for 'x':
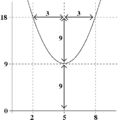
These are the x-coordinates where the graph crosses the x-axis. Also, the lowest or highest point of the graph, called the vertex, can be found from step 3. For this equation, the vertex is 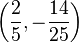 .
.
The quadratic formula
While completing the square works, there's an even more general way to solve any quadratic equation. This is called the "quadratic formula." It's a special formula where you just plug in the 'a', 'b', and 'c' values from your equation.
The quadratic formula is:
Remember, 'a', 'b', and 'c' are the numbers from your original equation: 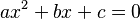 . This formula works for all quadratic equations. If 'a' were 0, it wouldn't be a quadratic equation anymore because the
. This formula works for all quadratic equations. If 'a' were 0, it wouldn't be a quadratic equation anymore because the 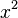 term would disappear.
term would disappear.
How the formula is proven
The quadratic formula itself comes from using the "completing the square" method, but with 'a', 'b', and 'c' instead of actual numbers. Here's how it's done:
- Step 1: Start with
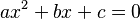 . Divide the entire equation by 'a'.
. Divide the entire equation by 'a'.
- Step 2: Move the
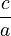 term to the other side.
term to the other side.
- Step 3: Complete the square on the left side by adding
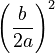 to both sides.
to both sides.
- The left side becomes a perfect square:
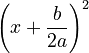 .
. - The right side can be combined into one fraction:
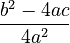 .
.
- So, we have:
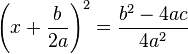
- So, we have:
- Step 4: Take the square root of both sides. Don't forget the
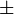 sign.
sign.
- Step 5: Move the
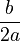 term to the other side to solve for 'x'.
term to the other side to solve for 'x'.
- Combine the terms on the right side since they have the same denominator:
And that's the quadratic formula!
Using the quadratic formula
Let's use the example from before: 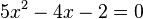 . Here, we can see that:
. Here, we can see that:
Now, plug these values into the quadratic formula: 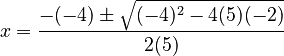
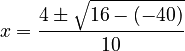
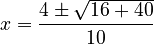
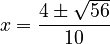
Solving this gives us the same two values for 'x' as before:
The quadratic formula is very powerful because it works for every quadratic equation.
The part inside the square root, 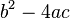 , is called the discriminant. It tells us about the roots of the equation:
, is called the discriminant. It tells us about the roots of the equation:
- If the discriminant is positive (greater than 0): There will be two different real values for 'x'. This means the graph crosses the x-axis at two separate points.
- If the discriminant is zero (equal to 0): There is only one real value for 'x'. This means the graph just touches the x-axis at its vertex, but doesn't cross it. It's like two roots that are exactly the same.
- If the discriminant is negative (less than 0): There are no real values for 'x'. On a graph, the parabola won't touch the x-axis at all. The roots in this case are complex numbers, which involve the imaginary unit 'i' (where
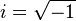 ).
).
Images for kids
-
The path of a cliff jumper follows a parabola because of how gravity works. This path can be described by a quadratic equation.
See also
 In Spanish: Ecuación de segundo grado para niños
In Spanish: Ecuación de segundo grado para niños