Factorization facts for kids

Factorization (also called factorisation or factoring) is like taking a big number and finding smaller numbers that multiply together to make it. These smaller numbers are called factors or divisors. For example, if you have the number 12, you can break it down into 3 and 4, because 3 multiplied by 4 equals 12. So, 3 and 4 are factors of 12. The number 1 is a factor of every number.

What is Prime Factorization?

When we talk about prime factorization, we break a number down into only prime numbers. A prime number is a number greater than 1 that can only be divided evenly by 1 and itself (like 2, 3, 5, 7, 11). Since 1 is not a prime number, it is not included in prime factorization.

For example, let's look at the number 12 again.

• You can factor 12 as 4 × 3. But 4 is not a prime number (it can be divided by 2).
• So, we break 4 down further: 4 is 2 × 2.
• This means the prime factorization of 12 is 3 × 2 × 2.
• We usually write the prime factors in order, from smallest to largest. So, 12 = 2 × 2 × 3.

Unique Prime Factors

Every number has its own special set of prime factors. This is called the Fundamental Theorem of Arithmetic. It means:

• Every number has one and only one unique set of prime numbers that multiply to make it.
• And every unique set of prime numbers multiplies to make one and only one number.

For example, the number 72 can be written as 2 × 2 × 2 × 3 × 3. This can also be shown using powers: 72 = 2³ × 3². No other combination of prime numbers will multiply to give 72.

This special fact is very important! It is used in cryptography, which is the science of keeping information secret. Finding the prime factors of very large numbers is extremely difficult for computers, which helps keep online information safe.

Factoring Polynomials

Factorization isn't just for regular numbers; it's also used in algebra to break down expressions called polynomials. Think of it like finding the building blocks of an algebraic expression.

Let's look at an example: 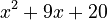Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2+9x+20

To factor this type of polynomial, we need to find two numbers that:

• Add up to the middle number (which is 9 in this case).
• Multiply together to get the last number (which is 20 in this case).

Can you think of two numbers that do this? The numbers are 4 and 5!

• 4 + 5 = 9
• 4 × 5 = 20

Now, we can rewrite the polynomial using these numbers: 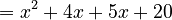Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): =x^2+4x+5x+20

Next, we group the terms: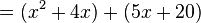

Then, we find what's common in each group and pull it out:

• In the first group (x² + 4x), both terms have 'x'. So, we pull out 'x': Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x(x+4)
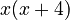
• In the second group (5x + 20), both terms can be divided by 5. So, we pull out '5': Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 5(x+4)

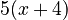
Now the expression looks like this: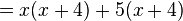

Notice that both parts now have 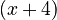Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (x+4) . We can pull that common part out too!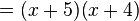

And there you have it! The polynomial 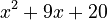Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2+9x+20 has been factored into 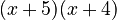Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (x+5)(x+4) . If you were to multiply 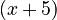Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (x+5) by Failed to parse (Missing <code>texvc</code> executable. 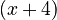Please see math/README to configure.): (x+4) , you would get the original polynomial back.

Related pages

• Fundamental theorem of arithmetic

See also

In Spanish: Factorización para niños