Parabola facts for kids
A parabola is a special kind of curve, or shape, that you can see in many places around you. The word "parabola" comes from the Greek word parabolē. This word means "application" or "comparison."
A long time ago, a Greek mathematician named Menaechmus (who lived around 380–320 BC) first found out about parabolas. Later, another Greek mathematician, Apollonius of Perga (who lived around 262 BC–c190 BC), was the first to give it the name "parabola."
Contents
What is a Parabola?
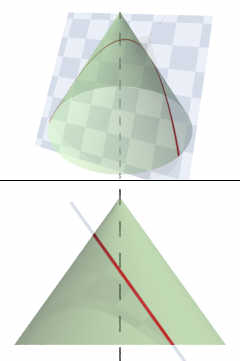
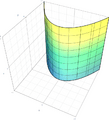
A parabola is part of a group of shapes called conic sections. These are shapes you get when you slice through a cone in different ways. Imagine you have a tall, pointed party hat. If you cut this hat with a flat knife, the shape you see on the cut surface is a conic section.
How a Parabola is Formed
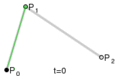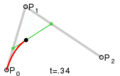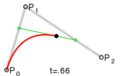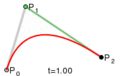
To make a parabola, you need to cut a cone in a very specific way. You cut the cone with a flat surface (a plane) that is parallel to one of the cone's slanted sides. The edge of the cut will then form a parabola.
The Vertex of a Parabola
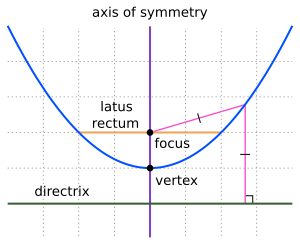
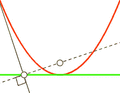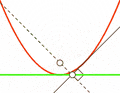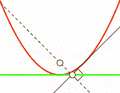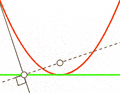
Every parabola has a special point called the vertex. This is the point where the curve changes direction. If the parabola opens upwards, the vertex is the lowest point. If it opens downwards, the vertex is the highest point. At the vertex, the curve is at its sharpest.
The Focal Point and Its Uses
Each parabola has a very important spot called the focal point (or focus). This point is like a special gathering place for light or sound waves.
How the Focal Point Works
Imagine a straight line that goes right through the middle of the parabola. This is called the axis of symmetry. If any ray (like a beam of light or a sound wave) comes into the parabola and is parallel to this axis, it will bounce off the curve and go straight through the focal point. This amazing property makes parabolas very useful!
Real-World Uses of Parabolas
Because of their unique reflective properties, parabolas are used in many cool devices:
- Satellite dishes: These dishes are shaped like parabolas. They collect weak signals from satellites far away and focus them all onto a small receiver at the focal point. This makes the signal strong enough to be used.
- Flashlights and car headlights: Here, the light source (bulb) is placed at the focal point. The parabolic mirror behind it reflects the light into a strong, parallel beam, making it shine far and bright.
- Magnifying mirrors: Some mirrors use a parabolic shape to focus light or heat, like in solar cookers that use the sun's energy to cook food.
- Microphones: Parabolic microphones can pick up sounds from far away by focusing sound waves onto a small microphone at the focal point.
The Parabola Equation
In mathematics, we can describe a parabola using an equation. The most common equation for a parabola is: 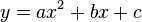 In this equation:
In this equation:
 and
and  are the coordinates of any point on the parabola.
are the coordinates of any point on the parabola.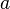 ,
, 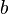 , and
, and  are numbers that stay the same for a specific parabola.
are numbers that stay the same for a specific parabola.- The number
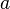 cannot be zero. If
cannot be zero. If 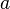 were zero, it would not be a parabola anymore, but a straight line!
were zero, it would not be a parabola anymore, but a straight line!
The value of 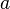 tells you if the parabola opens upwards or downwards, and how wide or narrow it is.
tells you if the parabola opens upwards or downwards, and how wide or narrow it is.
Images for kids
-
Parabolic compass designed by Leonardo da Vinci
-
A bouncing ball captured with a stroboscopic flash. The path it follows is very close to a parabola.
-
The supporting cables of suspension bridges often follow a curve that is similar to a parabola.
-
The Rainbow Bridge in Niagara Falls. The main arch is shaped like a parabola.
-
Solar cooker with a parabolic reflector to focus sunlight.
-
An array of parabolic troughs used to collect solar energy.
-
Edison's searchlight, which used a parabolic reflector.
-
Physicist Stephen Hawking in an aircraft flying a parabolic path to create a feeling of zero gravity.
See also
 In Spanish: Parábola (matemática) para niños
In Spanish: Parábola (matemática) para niños