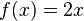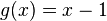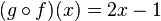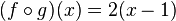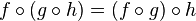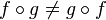Function composition facts for kids

In mathematics, function composition is a cool way to combine two or more functions to create a brand new one. Think of it like a chain reaction! The output of one function becomes the input for the next function in the chain.

Imagine you have a function f that takes something from a group called X and turns it into something in group Y. Then, you have another function g that takes something from group Y and turns it into something in group Z. When you "compose" g with f, written as g ∘ f, you get a new function that takes something directly from X and turns it into something in Z.

The value of function f for an input x is written as f(x). When you compose functions, the value of g ∘ f for an input x is written as (g ∘ f)(x). This means you first find f(x), and then you use that result as the input for g. So, (g ∘ f)(x) is the same as g(f(x)).

How Function Composition Works

Let's look at an example to make this clearer. Imagine we have two simple functions:

• Function f doubles a number (multiplies it by 2).
• Function g subtracts 1 from a number.

We can write these functions like this:

Composing g with f

If we compose g with f (written as g ∘ f), it means we first double the number, and then subtract 1 from the result. So, if you start with a number x:

1. First, f(x) doubles it to become 2x.
2. Then, g takes 2x and subtracts 1 from it, making it 2x - 1.

This new combined function is:

Composing f with g

Now, let's try composing f with g (written as f ∘ g). This means we first subtract 1 from the number, and then double the result. If you start with a number x:

1. First, g(x) subtracts 1, making it x - 1.
2. Then, f takes x - 1 and doubles it, making it 2(x-1).

This new combined function is:

Notice that the order really matters! 2x - 1 is not the same as 2(x-1). For example, if x is 2:

• (g ∘ f)(2) = 2*2 - 1 = 4 - 1 = 3
• (f ∘ g)(2) = 2*(2-1) = 2*1 = 2

Key Properties of Composition

Function composition has some interesting rules, just like addition or multiplication.

Associativity

Function composition is associative. This means that if you have three functions, say f, g, and h, it doesn't matter how you group them when you compose them. The final result will be the same. For example:

This means if you compose g with h first, and then compose f with that result, it's the same as composing f with g first, and then composing that result with h.

Commutativity

However, function composition is generally not commutative. This means that the order in which you compose functions usually changes the result. As we saw in our example:

This is why 2x - 1 was different from 2(x-1). The order of operations makes a big difference!

Related pages

• Chain rule

See also

In Spanish: Función compuesta para niños