Associativity facts for kids
The associative property is a cool idea in math that helps us understand how numbers work together. It's all about how you group numbers when you're doing operations like addition or multiplication.
Imagine you have three numbers you want to add. The associative property tells us that it doesn't matter which two numbers you add first. The final answer will always be the same!
For example, let's say you want to add 2, 5, and 10.
- You could add 2 and 5 first, then add 10:
* (2 + 5) + 10 = 7 + 10 = 17
- Or, you could add 5 and 10 first, then add 2:
* 2 + (5 + 10) = 2 + 15 = 17
See? Both ways give you 17! That's because addition is an associative operation. We can write this as: 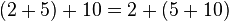
Contents
What is the Associative Property?
The associative property means that if you have three or more numbers and you're using the same operation (like all addition or all multiplication), the way you group the numbers with parentheses doesn't change the result. Think of it like this: you can "associate" (or group) the numbers differently, and it won't mess up your answer.
Associative Property in Addition
Addition is a great example of an associative operation. No matter how you group the numbers, the sum stays the same.
- If you have numbers a, b, and c, then:
* 
Let's try another example with addition:
- (3 + 4) + 7 = 7 + 7 = 14
- 3 + (4 + 7) = 3 + 11 = 14
Both ways give you 14!
Associative Property in Multiplication
Multiplication also follows the associative property. This means you can group the numbers differently when multiplying, and the product will be the same.
- If you have numbers a, b, and c, then:
* 
Let's look at an example:
- (2 × 3) × 4 = 6 × 4 = 24
- 2 × (3 × 4) = 2 × 12 = 24
Again, the answer is the same! This property is very useful when you have many numbers to multiply.
Operations That Are NOT Associative
Not all math operations are associative. Some operations give you a different answer if you group the numbers differently.
Subtraction is Not Associative
Subtraction is a good example of an operation that is not associative. Let's see why:
- Imagine you have the numbers 10, 5, and 2.
- If you group them like this:
* (10 - 5) - 2 = 5 - 2 = 3
- But if you group them differently:
* 10 - (5 - 2) = 10 - 3 = 7
As you can see, 3 is not the same as 7. So, subtraction is not associative. We write this as: 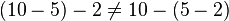
Division is Not Associative
Division is also not associative. The order in which you group the numbers matters a lot!
- Let's use 24, 6, and 2.
- If you group them like this:
* (24 ÷ 6) ÷ 2 = 4 ÷ 2 = 2
- But if you group them differently:
* 24 ÷ (6 ÷ 2) = 24 ÷ 3 = 8
Since 2 is not the same as 8, division is not an associative operation.
Associative vs. Commutative Property
It's easy to mix up the associative property with the commutative property, but they are different!
- The associative property is about grouping numbers. It asks: "Does it matter which numbers I do first?"
- The commutative property is about ordering numbers. It asks: "Can I swap the numbers around and still get the same answer?"
For example:
- Associative (grouping): (2 + 3) + 4 = 2 + (3 + 4)
- Commutative (ordering): 2 + 3 = 3 + 2
Both addition and multiplication are both associative and commutative. Subtraction and division are neither.
See also
 In Spanish: Asociatividad (álgebra) para niños
In Spanish: Asociatividad (álgebra) para niños

