Inverse function facts for kids
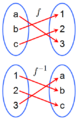
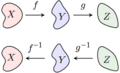
An inverse function is a special idea in mathematics. Imagine you have a function like a machine. You put something in (an input), and it gives you something out (an output). We often write this as 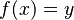 , where
, where  is the input and
is the input and  is the output.
is the output.
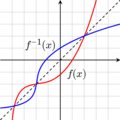
An inverse function does the exact opposite! It takes the output from the first function and turns it back into the original input. So, if 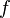 takes
takes  and gives you
and gives you  , its inverse function (often called
, its inverse function (often called 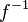 ) takes
) takes  and gives you
and gives you  back. This means
back. This means  . It's like an "undo" button for the first function. Don't mix up
. It's like an "undo" button for the first function. Don't mix up 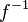 with
with 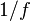 , which is a different idea called a reciprocal function.
, which is a different idea called a reciprocal function.
Contents
Understanding Inverse Functions
What an Inverse Function Does
Think of a function as a rule that changes one number into another. For example, if a function doubles a number, its inverse function would halve that number. If you start with 5, double it to get 10, then halve 10, you get 5 back. This is how inverse functions work.
Finding an Inverse Function
To find an inverse function, you can follow a simple trick. Let's say you have a function written as 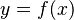 .
.
- First, swap the places of
 and
and  .
. - Then, solve the new equation to get
 by itself again.
by itself again.
For example, if your function is  (which means
(which means  is
is  multiplied by itself three times), to find its inverse:
multiplied by itself three times), to find its inverse:
- Swap
 and
and  :
:  .
. - Solve for
 : Take the cube root of both sides, so
: Take the cube root of both sides, so ![y = \sqrt[3]{x}](/images/math/3/0/5/3055a95564f016c3cb7958550ce93ffc.png) .
.
So, the inverse function of 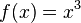 is
is ![f^{-1}(x) = \sqrt[3]{x}](/images/math/7/8/7/787a4594029c72e736448583d9724079.png) .
.
Another example: if  (this is a special function involving the number e):
(this is a special function involving the number e):
- Swap
 and
and  :
:  .
. - Solve for
 : Use the natural logarithm (written as
: Use the natural logarithm (written as 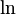 ), which is the inverse of
), which is the inverse of 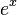 . So,
. So, 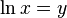 .
.
This shows that the inverse function of  is
is 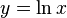 .
.
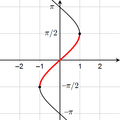
When Functions Don't Have Inverses
Not every function has a perfect inverse. For a function to have an inverse, each output must come from only one input. If two different inputs give the same output, the inverse function wouldn't know which input to go back to.
For example, consider the function 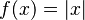 . This function gives you the positive value of any number.
. This function gives you the positive value of any number.
- If you put in -1, the output is 1 (
 ).
). - If you put in 1, the output is also 1 (
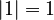 ).
).
If you tried to find an inverse for this, and you had the output 1, the inverse wouldn't know if it should give you -1 or 1 as the original input. Because of this, 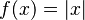 does not have an inverse function.
does not have an inverse function.
Sometimes, finding the inverse of a function can be very tricky!
Related pages
- Inverse element
- Inverse triangle function
- Inverse hyperbolic function
- Invertible matrix
Images for kids
See also
 In Spanish: Función inversa para niños
In Spanish: Función inversa para niños