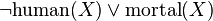Horn clause facts for kids

A Horn clause is a special kind of logical statement used in computer science and mathematics. It's like a rule that helps computers understand and solve problems. These clauses are named after Alfred Horn, who described them in 1951.

Think of a Horn clause as a sentence made of simple true/false statements, called "literals." In a Horn clause, at most one of these simple statements can be positive (meaning "true"), and all the others must be negative (meaning "not true").

Types of Horn Clauses

There are three main types of Horn clauses:

Definite Clause

A definite clause has exactly one positive statement. It's like saying, "If A, B, and C are true, then D must be true."

• Example: If you are a human, then you are mortal.

Fact

A fact is a definite clause with no negative statements. It's just a simple truth.

• Example: The sky is blue.

Goal Clause

A goal clause has no positive statements. It's often used to ask a question or state something that needs to be proven false.

• Example: Is it true that you are not human and not mortal? (This is usually phrased as trying to prove something is false).

How Horn Clauses Work in Logic

In logic, when we write a Horn clause, any variables in it (like 'X' in "human(X)") are usually considered to apply to "all" possible things.

For example, the statement:

Means:

For all X, if X is not human, or X is mortal.

This is the same as saying:

For all X, if X is human, then X is mortal.

Horn Clauses and Computers

Horn clauses are very important in computational logic and automated theorem proving. This means they help computers figure out if something is true or false, or solve logical puzzles.

When computers use a method called "resolution" to prove things, combining two Horn clauses always results in another Horn clause. This special property makes it easier and faster for computers to solve problems.

Logic Programming and Prolog

Horn clauses are the foundation of logic programming. This is a way of programming computers where you tell the computer facts and rules, and then ask it questions.

A common way to write definite clauses in logic programming is like a rule:

If (statement P is true AND statement Q is true AND ... AND statement T is true), THEN statement U is true.

This is often written in a backward way to show how it's used to solve problems:

U is true IF (P is true AND Q is true AND ... AND T is true).

The programming language Prolog uses this idea. In Prolog, the rule above would look like this:

`u :- p, q, ..., t.`

This means: "To figure out if 'u' is true, first figure out if 'p' is true, then if 'q' is true, and so on, until 't' is true." This is how Prolog solves problems by breaking them down into smaller goals.

Solving Problems Quickly

Propositional Horn clauses (which deal with simple true/false statements without variables) are also interesting in computational complexity. It's relatively easy and fast for computers to find out if a set of these clauses can all be true at the same time. This problem is called HORNSAT and can be solved very quickly.

However, if you add variables to Horn clauses (making them "first-order"), figuring out if they can all be true becomes much harder, sometimes even impossible for a computer to decide.

See also

In Spanish: Cláusula de Horn para niños