Image: Academ Base of trigonometry

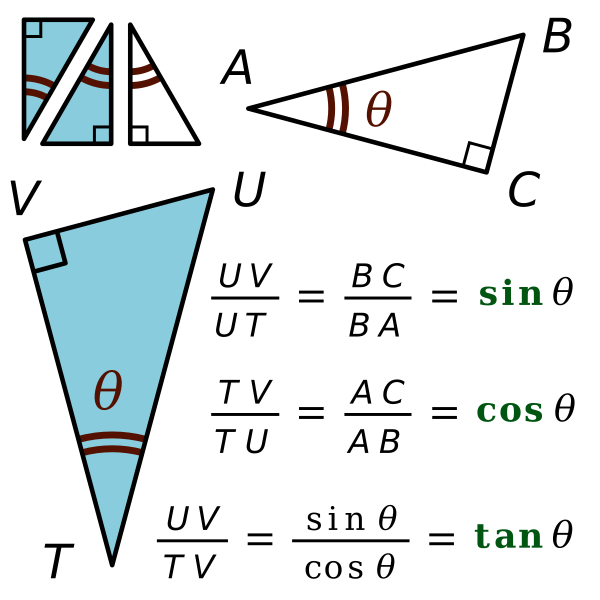
Description: Elementary trigonometry is based on this assert:  if two right triangles have equal acute angles, they are similar, so their side lengths are proportional.  This proportionality is the origin of trigonometry, because of the proportionality constants between side lengths of such triangles.  Three constants are written within the image, where θ  is the common measure of five acute angles.  For example,  tan θ  is a proportionality constant: the ratio of leg lengths of all right triangles similar to ABC,  provided that the numerator of the ratio is the leg opposite to the angle that measures θ. In a right triangle with an angle measuring θ,  a ratio of two side lengths only depends on the position of the sides relative to the angle that measures θ.  How to remember the position of each side relative to this angle, how to know assuredly the trigonometry formulas?  Here is a traditional mnemonic, like a magic formula to provide access to the three equalities:  SOH CAH TOA. Two similar right triangles are either directly or indirectly similar, except in case of isosceles triangles.  Within the image, they are directly similar if they have the same colour, otherwise they are indirectly similar.  To be clear, imagine a given triangle duplicated on a transparent tracing paper, to some scale.  If the original triangle and its copy are isosceles, the duplicate is the same on the transparent sheet, whatever the side that we see:  the front side or back side of the sheet, because of a mirror symmetry of the figure.  Such isosceles triangles are said both directly and indirectly similar.  Otherwise, the duplicate is either directly similar to the original or indirectly similar, depending on the side of the transparent sheet that we see.  To be more strict, a given similarity is either direct or indirect, according to the sign of its determinant.  For example, see the case of a determinant equal to –1.  
Title: Academ Base of trigonometry
Credit: Own work
Author: Baelde
Usage Terms: Creative Commons Attribution-Share Alike 3.0
License: CC BY-SA 3.0
License Link: https://creativecommons.org/licenses/by-sa/3.0
Attribution Required?: Yes