Trigonometric functions facts for kids

Basis of trigonometry: if two right triangles have equal acute angles, they are similar, so their corresponding side lengths are proportional.

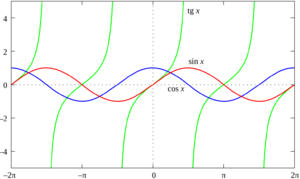
In mathematics, trigonometric functions are special functions that connect the angles of a right-angled triangle to the lengths of its sides. They are also called circular functions or angle functions. These functions are super useful in many areas of science and engineering, especially where geometry is involved. Think about things like navigation, building bridges, studying how planets move, and even understanding waves like sound or light. They are simple periodic functions, meaning their values repeat in a regular pattern. This makes them perfect for studying things that happen over and over again, like tides or sound waves.

The three most common trigonometric functions you'll learn about are the sine, the cosine, and the tangent. There are also three other functions that are their reciprocals: the cosecant, the secant, and the cotangent. These are used less often. Each of these six functions also has an inverse function that helps you find the angle if you know the side ratios.

Originally, these functions were defined using right-angled triangles, but only for angles smaller than 90 degrees. To use them for all angles, even negative ones or angles larger than 360 degrees, mathematicians started using a unit circle. This is a circle with a radius of 1 unit. Today, these functions can even be defined using infinite series or differential equations, which allows them to work with even more complex numbers.

Understanding Trigonometric Functions

Trigonometric functions help us find unknown angles or side lengths in triangles. They are especially useful for right-angled triangles.

How We Write Them

When we use trigonometric functions in math, we usually use short names for them.

"sin" for sine
"cos" for cosine
"tan" or "tg" for tangent
"sec" for secant
"csc" or "cosec" for cosecant
"cot" or "ctg" for cotangent

For example, you might see `sin(x)`. Sometimes, the parentheses are left out, like `sin x`. But if you're adding something to the angle, like `sin(x+y)`, the parentheses are important to show that `x+y` is the whole angle.

When you see a small number written above the function name, like `sin² x`, it means you multiply the function's value by itself. So, `sin² x` means `sin(x) * sin(x)`. It does NOT mean `sin(sin x)`.

However, if you see `sin⁻¹ x`, it means the inverse function of sine, also known as `arcsin x`. This function helps you find the angle if you know the sine value. For example, if `θ = sin⁻¹ x`, it means `sin θ = x`.

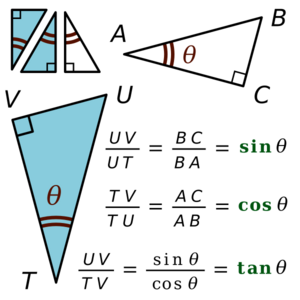
Right-Angled Triangle Basics

In this right triangle, with angle A: sin A = opposite/hypotenuse; cos A = adjacent/hypotenuse; tan A = opposite/adjacent.

Plot of the six trigonometric functions, the unit circle, and a line for the angle θ = 0.7 radians.

Imagine a right triangle with one angle called $θ$ (theta). If you have different right triangles but they all have the same angle $θ$ , they will be similar. This means the ratios of their side lengths will always be the same, no matter how big or small the triangles are. These six ratios are what define the six trigonometric functions.

In a right triangle:

The hypotenuse is the longest side, opposite the right angle.
The opposite side is across from the angle $θ$ .
The adjacent side is next to the angle $θ$ (but not the hypotenuse).

Here are the definitions:

Sine (sin):
Cosine (cos):
Tangent (tan):

The other three functions are the reciprocals of these:

Cosecant (csc): (which is $1/sin θ$ )
Secant (sec): (which is $1/cos θ$ )
Cotangent (cot): (which is $1/tan θ$ )

There are fun memory tricks to help you remember these definitions, like SOH CAH TOA!

In a right-angled triangle, the two acute angles (the ones less than 90 degrees) always add up to 90 degrees. This means that the sine of one acute angle is equal to the cosine of the other acute angle. For example, .

Radians vs. Degrees

Sine function on unit circle (top) and its graph (bottom)

When we talk about angles, we often use degrees. A right angle is 90°, and a full circle is 360°. This is common in everyday geometry.

However, in higher math and science, especially when dealing with calculus, angles are usually measured in radians. Radians are a more natural unit for math because they simplify many formulas.

One radian is the angle where the arc length around a unit circle is equal to the radius. It's about 57.3°. A full circle (360°) is equal to 2π radians (about 6.28 radians).

When you see `sin x` or `cos x` in advanced math, `x` is usually assumed to be in radians. If it's in degrees, you'll often see a degree symbol, like `sin x°`.

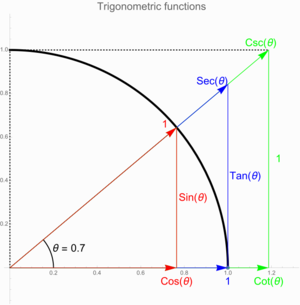
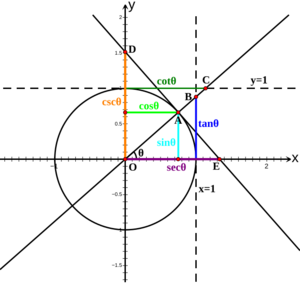
Unit Circle Definitions

All of the trigonometric functions of the angle

θ

(theta) can be drawn using a unit circle.

In this picture, the six trigonometric functions of an angle

θ

are shown as coordinates of points on the unit circle.

Signs of trigonometric functions in each quadrant. The mnemonic "all science teachers (are) crazy" helps remember when sine, cosine, and tangent are positive from quadrants I to IV.

The unit circle is a circle with a radius of 1, centered at the origin (0,0) of a graph. Using the unit circle helps us define trigonometric functions for *any* angle, not just angles in a right triangle.

Imagine a line starting from the center of the circle and going along the positive x-axis. Now, rotate this line by an angle $θ$ .

If you rotate counter-clockwise, $θ$ is positive.
If you rotate clockwise, $θ$ is negative.

The point where this rotated line crosses the unit circle is called point A (x, y).

The cosine of the angle $θ$ is the x-coordinate of point A ().
The sine of the angle $θ$ is the y-coordinate of point A ().

Since point A is on the unit circle, its coordinates (x, y) must follow the equation . This leads to a very important identity:

(This is called the Pythagorean identity because it comes from the Pythagorean theorem!)

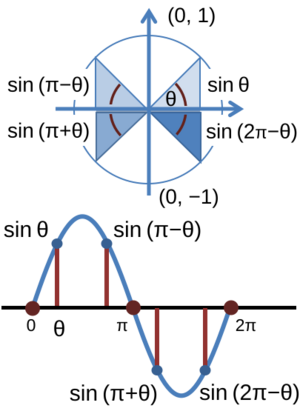
Because rotating by a full circle (360° or 2π radians) brings you back to the same spot, sine and cosine values repeat every 360° (or 2π radians). This means they are periodic functions with a period of 2π.

(Here, $k$ can be any whole number).

The tangent and cotangent functions repeat every 180° (or π radians).

Common Angle Values

It's helpful to know the exact values of sine, cosine, and tangent for some common angles. These values often involve square roots.

Here are some values for angles from 0° to 90°:

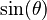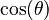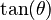Angle, θ, in		$\sin(\theta)$	$\cos(\theta)$	$\tan(\theta)$
radians	degrees	$\sin(\theta)$	$\cos(\theta)$	$\tan(\theta)$
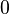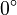$0$	$0^\circ$	$0$	$1$	$0$
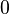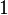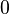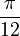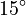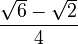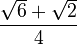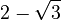$\frac{\pi}{12}$	$15^\circ$	$\frac{\sqrt{6}-\sqrt{2}}{4}$	$\frac{\sqrt{6}+\sqrt{2}}{4}$	$2-\sqrt{3}$
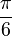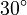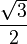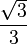$\frac{\pi}{6}$	$30^\circ$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{3}$
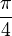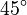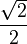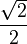$\frac{\pi}{4}$	$45^\circ$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	$1$
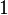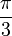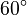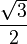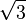$\frac{\pi}{3}$	$60^\circ$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
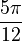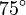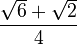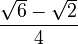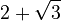$\frac{5\pi}{12}$	$75^\circ$	$\frac{\sqrt{6}+\sqrt{2}}{4}$	$\frac{\sqrt{6}-\sqrt{2}}{4}$	$2 + \sqrt{3}$
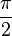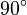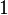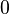$\frac{\pi}{2}$	$90^\circ$	$1$	$0$	Undefined

Basic Rules (Identities)

There are many important rules, called identities, that connect trigonometric functions. Here are some of the most basic ones. You can prove these rules using the unit circle or right-angled triangles.

Even and Odd Functions

Some functions are "even" and some are "odd."

Cosine and secant are even functions. This means if you put a negative angle in, you get the same result as a positive angle:

* *

The other trigonometric functions (sine, tangent, cotangent, cosecant) are odd functions. This means if you put a negative angle in, you get the negative of the result for a positive angle:

* * * *

Pythagorean Identity

This is one of the most important identities, coming directly from the Pythagorean theorem and the unit circle:

You can get two other identities by dividing this one:

Sum and Difference Formulas

These formulas help you find the sine, cosine, or tangent of an angle that is the sum or difference of two other angles.

Sum:

* * *

Difference:

* * *

If the two angles are the same (), these formulas simplify into "double-angle formulas":

Inverse Functions

Graphs of sine, cosine and tangent.

Since trigonometric functions repeat their values (they are periodic), they don't have a simple "inverse" that works for all angles. However, we can define inverse functions if we limit the range of angles we are looking at. These are called inverse trigonometric functions or "arc functions."

For example, `arcsin x` (or `sin⁻¹ x`) tells you the angle whose sine is `x`. Here are the main inverse functions and their usual ranges:

Function	Definition	Input Range	Output Range (Principal Values)
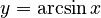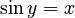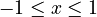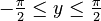$y = \arcsin x$	$\sin y = x$	$-1 \le x \le 1$	${\textstyle -\frac{\pi}{2} \le y \le \frac{\pi}{2}}$
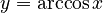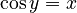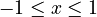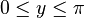$y = \arccos x$	$\cos y = x$	$-1 \le x \le 1$	${\textstyle 0 \le y \le \pi}$
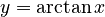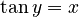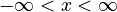$y = \arctan x$	$\tan y = x$	$-\infty < x < \infty$	${\textstyle -\frac{\pi}{2} < y < \frac{\pi}{2}}$
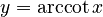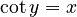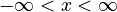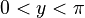$y = \arccot x$	$\cot y = x$	$-\infty < x < \infty$	${\textstyle 0 < y < \pi}$
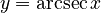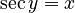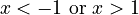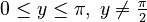$y = \arcsec x$	$\sec y = x$	$x<-1 \text{ or } x>1$	${\textstyle 0 \le y \le \pi,\; y \ne \frac{\pi}{2}}$
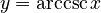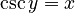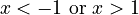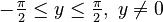$y = \arccsc x$	$\csc y = x$	$x<-1 \text{ or } x>1$	${\textstyle -\frac{\pi}{2} \le y \le \frac{\pi}{2},\; y \ne 0}$

Using "arc" (like `arcsin`) helps avoid confusion with `sin⁻¹`, which might look like `1/sin`.

Real-World Uses

Trigonometric functions are not just for math class; they have many practical uses!

Angles and Sides of a Triangle

Trigonometry is super helpful for figuring out unknown angles or side lengths in any triangle, not just right triangles. We use special rules for this. Let's say a triangle has angles A, B, C and sides opposite them named a, b, c.

Law of Sines

The Law of sines says that the ratio of a side length to the sine of its opposite angle is the same for all three sides of any triangle: 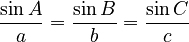Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}} This law is great for finding unknown side lengths if you know two angles and one side. It's used in triangulation, a method to find distances by measuring angles from two known points.

Law of Cosines

The Law of cosines is like an extended version of the Pythagorean theorem for any triangle: 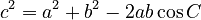Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle c^2=a^2+b^2-2ab\cos C} This rule helps you find a side length if you know two sides and the angle between them. It can also help you find an angle if you know all three side lengths.

Other Laws

There are also the Law of tangents and the Law of cotangents, which provide more ways to relate the sides and angles of a triangle.

Periodic Patterns

A Lissajous curve, a figure formed with a trigonometry-based function.

An animation of the additive synthesis of a square wave with an increasing number of harmonics.

Trigonometric functions are very important in physics. Sine and cosine, for example, describe simple harmonic motion. This is how many things in nature move, like a weight bouncing on a spring or a pendulum swinging (for small swings). They are like the one-dimensional shadows of something moving in a circle.

These functions are also key to understanding any periodic function – anything that repeats in a regular pattern. The wave shapes of sine and cosine are perfect for modeling things like sound waves or light waves.

Using something called a Fourier series, we can break down almost any repeating pattern into a sum of simple sine and cosine waves. This helps scientists and engineers understand and create complex signals, like music or radio waves.

History of Trigonometry

The study of trigonometry started a very long time ago. Early ideas came from ancient civilizations like the Greeks.

The idea of the "chord" function was used by Hipparchus (around 180–125 BCE) and Ptolemy (around 90–165 CE). Later, in ancient India, the "sine" and "versine" functions were developed. These ideas then traveled to the Islamic world.

By the 9th century, all six trigonometric functions we use today were known in Islamic mathematics. Arab mathematicians like Al-Khwārizmī and Muhammad ibn Jābir al-Harrānī al-Battānī created tables for these functions and discovered rules like the law of sines.

The terms tangent and secant were first used by the Danish mathematician Thomas Fincke in 1583. The abbreviations "sin", "cos", and "tan" were first published by the French mathematician Albert Girard in the 17th century.

Later, in the 18th century, Leonhard Euler showed how sine and cosine are connected to the exponential function. He also gave us the modern abbreviations we use today.

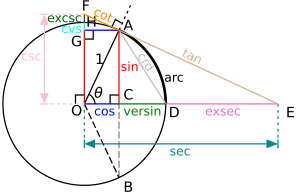
Some older trigonometric functions, like the versine or haversine, are not used much anymore, but they were important in the past, especially for navigation.

What the Words Mean

The word sine comes from the Latin word sinus, which means "bend" or "bay." It was chosen because of a misunderstanding of an Arabic word that meant "pocket" or "fold." This Arabic word itself came from a Sanskrit word meaning "bowstring."
The word tangent comes from the Latin word tangens, meaning "touching." This makes sense because the tangent line "touches" the unit circle.
The word secant comes from the Latin word secans, meaning "cutting." This is because the secant line "cuts" through the unit circle.
The prefix "co-" (in cosine, cotangent, cosecant) was first used in 1620. It means "complementary sine," referring to the sine of the complementary angle (the angle that adds up to 90 degrees).

Images for kids

Top: Trigonometric function $sin θ$ for selected angles $θ$ , $π - θ$ , $π + θ$ , and $2 π - θ$ in the four quadrants.
Bottom: Graph of sine function versus angle. Angles from the top panel are identified.
The unit circle, with some points labeled with their cosine and sine (in this order), and the corresponding angles in radians and degrees.

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:

Trigonometric functions Facts for Kids. Kiddle Encyclopedia.