Inflection point facts for kids
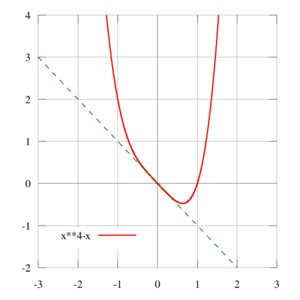
An inflection point is a special spot on a curve (like a line you draw on a graph) where the curve changes how it bends. Imagine you're driving a car along a curvy road. At an inflection point, the road changes from bending one way to bending the other way.
Think of it this way: * A curve can be concave up (like a bowl holding water, or a smile). * A curve can be concave down (like an upside-down bowl, or a frown).
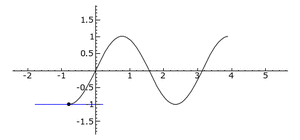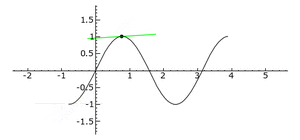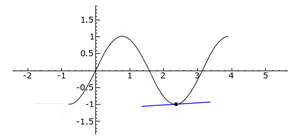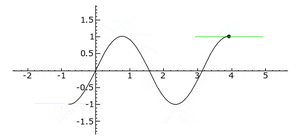
An inflection point is exactly where the curve switches from being concave up to concave down, or from concave down to concave up. It's a bit like the point where a roller coaster track changes from going up a hill to going down, or vice versa, but specifically about the way the curve bends.
An undulation point is similar to an inflection point, but the curve doesn't actually change its overall bending direction. It might flatten out for a moment, but then continue bending in the same way it was before. It's a more advanced concept, but you can think of it as a brief pause in the bending change.
== Understanding Curves and Bends == When we talk about curves in math, we often mean lines drawn on a graph. These lines can represent many things, like how fast something is moving, how a population is growing, or even the shape of a bridge.
=== What is Concave Up? === A curve is concave up when it looks like a valley or a bowl. If you were to place a ball on this part of the curve, it would roll towards the middle. Think of the letter "U" or the bottom part of a smile.
=== What is Concave Down? === A curve is concave down when it looks like a hill or an upside-down bowl. If you placed a ball on this part of the curve, it would roll away from the middle. Think of an upside-down "U" or the top part of a frown.
== Finding Inflection Points == In higher-level math, like calculus, mathematicians use special tools to find inflection points. They look at how the slope of the curve is changing. The slope tells you how steep the curve is at any given point.
* When a curve is concave up, its slope is increasing (getting steeper upwards). * When a curve is concave down, its slope is decreasing (getting flatter or steeper downwards).
An inflection point is where the rate of change of the slope itself changes. It's a point where the curve's "bendiness" switches direction.
== Real-World Examples == Inflection points might seem like a purely mathematical idea, but they show up in many real-world situations:
* Roller Coasters: The design of a roller coaster track involves many curves. Inflection points would be where the track switches from curving one way to curving the opposite way, making the ride exciting! * Economics: In business, graphs might show how a company's sales are growing. An inflection point could indicate where the rate of sales growth starts to slow down, even if sales are still increasing overall. * Science: In physics or chemistry, graphs showing how a reaction progresses over time might have inflection points, indicating a change in the rate of the reaction.
== See also ==  In Spanish: Punto de inflexión para niños
In Spanish: Punto de inflexión para niños