Loop (graph theory) facts for kids
In the world of graph theory, a loop is a special kind of connection. Imagine you have a point, called a vertex, and a line, called an edge. A loop is simply an edge that starts at a vertex and then connects right back to that very same vertex. It's like a road that leaves a town and immediately returns to it without visiting any other towns.
Contents
What is Graph Theory?
Graph theory is a fascinating part of mathematics that studies how things are connected. It uses simple pictures called graphs to show these connections. A graph is made up of two main parts:
- Vertices (also called nodes): These are the points or dots in the graph. Think of them as locations, people, or objects.
- Edges (also called links): These are the lines that connect the vertices. They show relationships, roads, or communication paths between the locations or objects.
Why Do We Use Graphs?
Graphs are super useful! They help us understand and solve problems in many areas, like:
- Computer science: How computers are connected in a network.
- Social media: How friends are connected on platforms like Facebook.
- Transportation: How roads connect cities or how flights connect airports.
- Biology: How different species interact in an ecosystem.
Understanding Loops in Graphs
A loop is a unique type of edge because it doesn't connect two different vertices. Instead, it connects a vertex to itself.
How Do Loops Look?
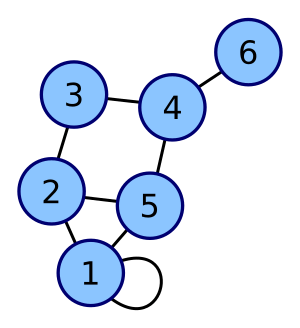
On a drawing of a graph, a loop looks like a small circle or a curved line that starts and ends at the same vertex. The image at the top of this page shows a clear example of a loop on vertex 1.
When Do We See Loops?
Loops might seem a bit strange at first, but they are important in certain situations:
- Self-relationships: Sometimes, a loop can represent a relationship an item has with itself. For example, in a social network graph, a loop on a person's vertex might show that they have a personal blog or a diary.
- Computer networks: In some network diagrams, a loop might show a device that can send data to itself.
- State machines: In computer science, loops can represent a system staying in the same state or condition.
Types of Graphs and Loops
Not all graphs allow loops. Graphs are often categorized based on whether they can have loops or multiple edges between the same two vertices.
Simple Graphs
A simple graph is a graph that does not have any loops. It also doesn't have more than one edge connecting the same pair of vertices. Simple graphs are common in many basic graph theory problems.
Multigraphs
A multigraph is a type of graph that can have loops. It can also have multiple edges between the same two vertices. Multigraphs are used when you need to show more complex connections, like multiple roads between two cities or different types of relationships between two people.
Importance of Loops
Loops are a fundamental concept in graph theory, helping mathematicians and computer scientists model and understand various real-world situations. They add flexibility to how we represent connections and relationships, making graph theory a powerful tool for solving problems.
