Magma (algebra) facts for kids
In abstract algebra, a magma is a basic kind of algebraic structure. Think of it as a set of things that has one special rule, called a binary operation. This rule tells you how to combine any two things from the set to get another thing that is also in the set. No other special rules are needed for a magma.
Contents
What is a Magma?
A magma is made of two parts:
- A set of elements, let's call it M.
- A binary operation, often shown as •. This operation takes any two elements from M and combines them to make a third element.
To be a magma, this combination rule must follow one important requirement:
- Closure: When you combine any two elements from the set M using the operation •, the result must always be another element that is also in M.
In math language, this means:
- For any elements a and b in M, the result of a • b is also in M.
If the operation doesn't always work for every pair of elements, it's called a partial magma.
How Magmas Got Their Name
The word groupoid was first used in 1927 by Heinrich Brandt. Later, in 1937, B. A. Hausmann and Øystein Ore used groupoid to mean what we now call a magma. However, this caused some confusion because Brandt's original idea of a "groupoid" was different.
The term magma was later used by famous mathematicians like Jean-Pierre Serre in 1965 and in books by Nicolas Bourbaki. This word helped avoid the confusion with the term groupoid.
How We Write Magma Operations
When you use the magma operation many times, the order can matter. We use parentheses to show which operations happen first. For example, if you have a, b, c, and d, you might write:
- (a • (b • c)) • d
Sometimes, the operation symbol • is left out, and we just write the elements next to each other, like:
- (a(bc))d
There are also other ways to write these operations without using many parentheses, like prefix notation or postfix notation (also known as reverse Polish notation), which are often used in computer science.
The number of different ways to group elements when you have n operations in a magma is given by special numbers called Catalan numbers. For example, with two operations and three elements (like a, b, c), there are two ways to group them: (ab)c and a(bc).
Free Magmas
Imagine you have a set of basic building blocks, like letters. A free magma made from these blocks is like creating all possible "words" or combinations using these blocks and the magma operation, without any extra rules. You just combine them by putting them together and adding parentheses.
For example, if your blocks are a and b:
- a • b can be written as (a)(b)
- a • (a • b) can be written as (a)((a)(b))
Think of a free magma as a collection of all possible binary trees where the leaves (the ends of the branches) are your basic building blocks. The magma operation is like joining two trees at their roots. This idea is very important in computer science for understanding how programming code is structured.
Types of Magmas
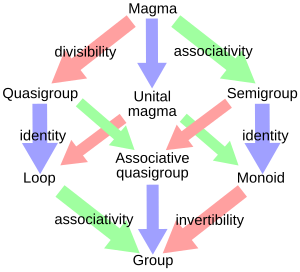
Magmas are the most basic algebraic structures. Often, mathematicians study magmas that have extra rules or properties. Here are some common types of magmas:
- Quasigroup: A magma where you can always "undo" an operation. This is like being able to divide in regular numbers.
- Loop: A quasigroup that also has an identity element. An identity element is like the number 0 for addition (adding 0 doesn't change the number) or 1 for multiplication (multiplying by 1 doesn't change the number).
- Semigroup: A magma where the operation is associative. This means that the way you group elements doesn't change the result. For example, (a • b) • c is the same as a • (b • c).
- Monoid: A semigroup that also has an identity element.
- Group: This is a very important type of algebraic structure. A group is a magma that has an identity element, is associative, and every element has an inverse (something that "undoes" it).
Magmas with Special Properties
Magmas can have many other interesting properties. Here are a few:
- Commutative: If the order of the elements doesn't matter. So, a • b is always the same as b • a. (Like addition: 2 + 3 = 3 + 2).
- Idempotent: If combining an element with itself gives you the element back. So, a • a is always a.
- Alternative: If certain ways of grouping three elements always give the same result, even if the magma is not fully associative.
- Flexible: If (a • b) • a is always the same as a • (b • a).
- Unital: If it has an identity element.
See also
 In Spanish: Magma (álgebra) para niños
In Spanish: Magma (álgebra) para niños
- Universal algebra
- Commutative magma
- Algebraic structures whose axioms are all identities