Masyu facts for kids

A Masyu puzzle ready to be solved. Can you figure it out?

The solution to the Masyu puzzle shown above.

Masyu (pronounced Mashu) is a fun logic puzzle from Japan. The name "Masyu" means "evil influence." It was created by a company called Nikoli. What makes Masyu special is that it doesn't use any numbers or letters. Instead, you solve it by drawing a single line! It's all about thinking logically and using visual clues.

How to Play Masyu

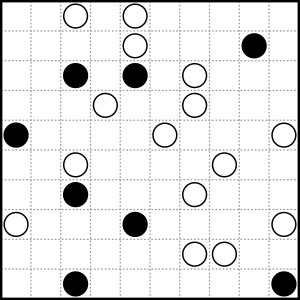
Masyu puzzles are played on a grid of squares. Some of these squares have circles in them. These circles can be either "white" (empty) or "black" (filled).

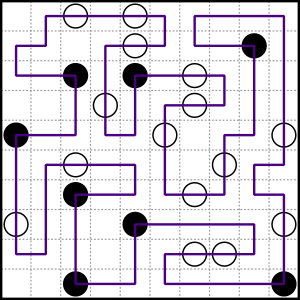
Your main goal is to draw a single, continuous line that forms a loop. This loop must go through every single circle on the grid. The line can't cross itself, and it must enter and exit each square from the middle of its sides. This means all turns you make will be at a 90-degree angle.

The two types of circles have different rules for how your loop must pass through them:

• White circles: When your loop goes through a white circle, it must go straight. However, the loop must make a turn in the square before the white circle, or in the square after it, or both!
• Black circles: When your loop goes through a black circle, it must make a turn inside that circle. But, the loop must go straight through the square before the black circle and the square after it.

Different Kinds of Masyu Puzzles

Sometimes, Masyu puzzles come with extra twists to make them even more challenging:

• Gray Circles: Some puzzles have gray circles. You have to figure out if each gray circle should act like a white circle or a black circle.
• Donut Grids: Imagine the grid is like a donut! The left and right edges are connected, and so are the top and bottom edges. This means your loop can wrap around the puzzle.
• Region Puzzles: The grid might be split into different areas. In these puzzles, your loop must make at least one turn in every single area.
• Hexagon Grids: Instead of squares, some Masyu puzzles use a grid of hexagons. The rules for turns change to 60-degree or 120-degree angles.

Smart Ways to Solve Masyu

Solving Masyu puzzles is all about understanding how the circles work together. It's often easiest to start solving from the edges of the grid and then work your way inwards. Here are some helpful tips:

Starting with Black Circles

Black circles are great starting points because they have strict rules:

• Any line coming out of a black circle must go straight for two squares. It can't hit another part of your loop or the edge of the puzzle.
• Each black circle must have two lines coming out of it that meet at a right angle.
• If you can't draw a line two squares in one direction from a black circle (maybe because of the border), then the line must go in the opposite direction for two squares.
• Black circles near the border: If a black circle is on the very edge or one square away from the edge, its line must go away from that border. If it's near a corner, lines must go away from both borders.
• Two black circles next to each other: If two black circles are right next to each other, the lines coming out of them must go away from each other.

Using White Circles to Your Advantage

White circles also give you important clues:

• White circles on the border: If a white circle is on the edge of the grid, the loop must go straight through it, parallel to the border.
• Adjacent white circles: If two white circles are next to each other on a border, or one square apart, the loop will need to turn away from the border just after these circles.
• Three or more white circles in a row: If you see three or more white circles in a straight line, the loop must pass through each of them straight, going across the line of circles.

Advanced Solving Tips

• Black circle with diagonal white circles: If a black circle has two white circles diagonally next to it on the same side, the loop must go away from that side. If it went between the white circles, it would be impossible to complete the black circle's rules.
• Avoiding "Short Circuits": Remember, your final answer must be a single, continuous loop. As you draw lines, make sure you don't accidentally close off a small loop too early. This would prevent you from completing the entire puzzle.

Masyu puzzles can be quite tricky, but they are always designed so you can solve them with careful thought and logic.