Maze generation algorithm facts for kids

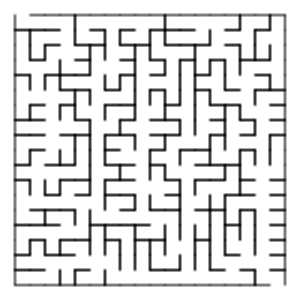
Maze generation algorithms are like special computer recipes that create mazes automatically. These recipes help computers build all sorts of mazes, from simple ones to super tricky puzzles!

This maze was made using a special version of Prim's algorithm.

How Computers Build Mazes

This animation shows a computer building a maze using a graph theory method.

Imagine a maze as a grid of cells, like a big checkerboard. Each cell has walls around it. Maze-making programs start with this grid. They then decide which walls to remove to create paths.

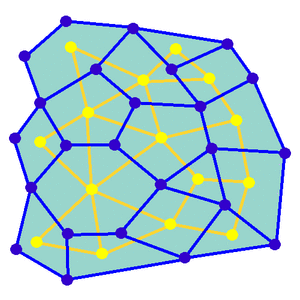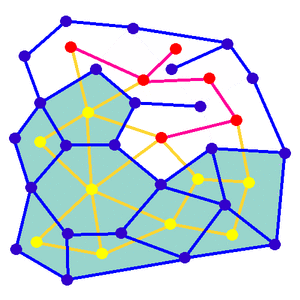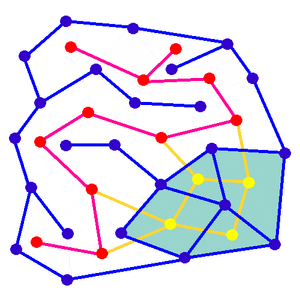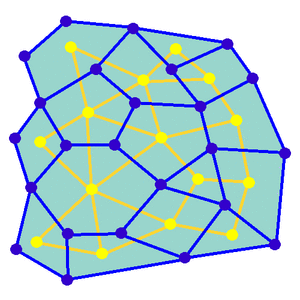
Think of the cells as "nodes" and the possible walls between them as "edges" in a network. The goal of a maze-making program is to remove some edges (walls) so you can find a path from one point to another.

If the maze isn't "connected," it means some parts are cut off. You can't reach them. If the maze has "loops," it means there's more than one way to get from one spot to another. Most maze programs try to create a "perfect" maze. This means it's connected, and there's only one path between any two points. This makes the maze a bit harder to solve!

The animation shows a maze being built. First, the computer makes a random network (graph) of blue lines. Then, it uses a special search method to draw a red path. As the red path crosses a blue line, that blue line (wall) is removed. When the path is done, the red lines disappear, leaving the maze.

Recursive Backtracker: A Simple Maze Builder

This method is also called the "recursive backtracker." It's one of the easiest ways for a computer to make a maze.

Imagine your maze space as a big grid of cells. Each cell starts with all four walls.

1. Start Anywhere: The computer picks a random cell to begin. 2. Explore: It looks for a neighbor cell that hasn't been visited yet. 3. Break a Wall: If it finds an unvisited neighbor, it removes the wall between the current cell and the new one. 4. Move On: The new cell is now marked as visited. The computer moves to this new cell and remembers its path. 5. Dead End: If a cell has no unvisited neighbors, it's a dead end! The computer then "backtracks." It goes back along the path it came from until it finds a cell with an unvisited neighbor. 6. Keep Going: It then starts exploring again from that new spot. 7. Finish: This continues until every single cell in the maze has been visited. This makes sure the maze is fully connected.

Mazes made with this method often have long, winding corridors. This is because the computer tries to go as far as possible in one direction before turning back.

How the Computer Does It (Step-by-Step)

This method often uses a technique called "recursion." Think of recursion as a set of instructions that keeps calling itself until a task is done.

• The computer starts at a cell. It marks this cell as visited.
• Then, it keeps doing this:

* If the current cell has any neighbors it hasn't visited yet: * It picks one of those unvisited neighbors. * It removes the wall between the current cell and the chosen neighbor. * It then repeats the whole process for the chosen neighbor.

This process keeps going until all cells are visited.

Another Way to Do It (No Deep Recursion)

Sometimes, using too much recursion can cause problems for a computer. So, there's another way to do the same thing without going too deep. This method uses a "stack," which is like a pile of plates. You add plates to the top, and you can only take plates from the top.

• Pick a starting cell, mark it as visited, and put it on the stack.
• While there are still cells on the stack:

* Take a cell from the top of the stack. This is your current cell. * If this current cell has any unvisited neighbors: * Put the current cell back on the stack (you might need to come back to it). * Choose one of the unvisited neighbors. * Remove the wall between the current cell and the chosen neighbor. * Mark the chosen neighbor as visited and put it on the stack.

This maze has more horizontal paths.

Kruskal's Algorithm: Building with Walls

This method is a random version of something called "Kruskal's algorithm."

1. List All Walls: First, the computer makes a list of every single wall in the grid. 2. Separate Cells: Each cell is also put into its own separate group. 3. Random Walls: The computer then picks walls from the list in a random order. 4. Check Groups: For each wall, it checks if the two cells on either side of the wall belong to different groups. 5. Remove Wall & Join Groups: If they are in different groups, the computer removes that wall. Then, it joins the two groups of cells into one big group. 6. Keep Going: This continues until all cells are part of the same big group.

Mazes made with Kruskal's algorithm often have patterns that are quite regular. This can sometimes make them easier to solve.

Prim's Algorithm: Growing the Maze

This method is a random version of "Prim's algorithm."

1. Start with Walls: Begin with a grid where all the walls are in place. 2. Pick a Cell: Choose any cell and mark it as part of the maze. Add all the walls around this cell to a special "wall list." 3. Grow the Maze: While there are still walls in the wall list: * Pick a random wall from the list. * Check if only one of the two cells that the wall divides is already part of the maze. * If yes, remove that wall to create a path. Mark the unvisited cell as part of the maze. * Add the walls around this newly added cell to your wall list. * Remove the wall you just used from the list.

This method tends to create mazes where it's easier to find your way back to the starting point.

A Simpler Prim's Version

There's an even simpler way to use Prim's idea:

• Instead of tracking all walls, just keep a list of cells that are next to the maze you're building.
• Randomly pick one of these neighboring cells.
• Connect it to the maze.

This version might create a few more branches in the maze.

Wilson's Algorithm: Truly Random Mazes

The methods above can sometimes create mazes with certain "styles." For example, the recursive backtracker makes long corridors. Wilson's algorithm, however, creates truly random mazes. It makes sure every possible maze has an equal chance of being created.

1. Start Small: Begin the maze with just one cell, chosen randomly. 2. Random Walk: Pick a new cell that's not yet in the maze. Start a random walk from this cell. 3. Erase Loops: If your random walk ever crosses its own path, forming a loop, erase that loop! Keep walking. 4. Join the Maze: When your walk finally reaches a cell that's already part of the maze, add your entire loop-erased path to the maze. 5. Fill It Up: Keep doing this from new, unvisited cells until every cell is part of the maze.

This method ensures the maze is perfectly random, no matter how you pick the starting cells for your walks.

Aldous-Broder Algorithm: Another Random Maze Builder

This algorithm also creates truly random mazes.

1. Start: Pick a random cell to begin and mark it as visited. This is your "current" cell. 2. Keep Going: While there are still cells that haven't been visited: * Pick a random neighbor of your current cell. * If this chosen neighbor has not been visited yet: * Remove the wall between your current cell and the chosen neighbor. * Mark the chosen neighbor as visited. * Make the chosen neighbor your new current cell.

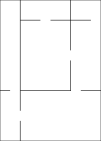
Recursive Division: Dividing the Space

How Recursive Division Works

Start	Divide with walls	Add openings	Keep dividing	Finished!
step 1	step 2	step 3	step 4	step 5

Mazes can also be made using "recursive division." This method works like this:

1. Big Empty Room: Start with a big, empty space, like a large room. 2. Add Walls: Divide this room with a randomly placed wall (or a few walls). Each wall needs a random opening (a door) in it. 3. Repeat: Now, treat each of the smaller rooms you just made as new, empty spaces. Repeat the process: divide them with walls and add openings. 4. Smallest Rooms: Keep doing this until all the "rooms" are as small as possible, like single cells.

This animation shows a maze being built using recursive division.

This method often creates mazes with long, straight walls. This can sometimes make it easier to see which parts of the maze to avoid.

For example, in a square maze, you might put two walls that cross each other. This divides the big room into four smaller rooms. Then, you choose three of those four walls and make a small opening in each. You keep doing this for the smaller rooms until they are all just one cell wide.

Simple Maze Algorithms

This is a 3D maze made with Prim's algorithm.

Some maze-making methods are very simple. They don't need to remember a lot of information about the whole maze at once.

One example is the "Sidewinder algorithm." It starts by making an open path all the way across the top row of the maze. For the rows below, it creates short horizontal paths. Each of these paths has one connection going up to the path above it. This makes the Sidewinder maze very easy to solve if you start from the bottom and go up, because there are no dead ends going upwards.

Another simple one is the "binary tree maze." In this type of maze, each cell always has a path leading either up or to the left, but never both. To make one, for each cell, you flip a coin. If it's heads, you add a path going up. If it's tails, you add a path going left. If you always pick the same direction for cells on the edges, you'll get a working maze. Like the Sidewinder maze, it's easy to solve in the direction of the bias (up and left).

You can also make patterns that look like mazes by randomly putting forward slash (/) and backslash (\) characters. This doesn't make a "perfect" maze you can solve, but it creates cool-looking loops and paths.

Images for kids

• 

  A different animation of a maze being made with depth-first search.

• 

  A maze made on an old computer called the Commodore 64.