Maze solving algorithm facts for kids
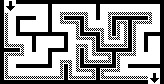
Imagine you're lost in a giant maze. How would you find your way out? People and even computers use special methods, called maze solving algorithms, to figure out the path. Some methods are for when you're inside the maze and can't see the whole thing. Others are for when you can see the entire maze from above, like on a map.
Mazes that don't have any loops are called "perfect" mazes. They are like a tree with branches. Many maze-solving methods are based on ideas from graph theory, which is a way to study connections between things.
Contents
Random Mouse Algorithm
This is a super simple way to solve a maze. Imagine a very basic robot or even a mouse trying to find its way. It just walks straight until it hits a junction (where paths meet). Then, it randomly picks a direction to go next.
This method will always eventually find the exit. However, it can be incredibly slow! It might wander around for a very long time before getting out.
Wall Follower Method
The most famous maze-solving trick is the wall follower. You might know it as the left-hand rule or right-hand rule. Here's how it works:
If the maze walls are all connected (like one big loop or connected to the outside), you just keep one hand (say, your right hand) touching a wall. You walk forward, always keeping that hand on the wall. If there's an exit, you are guaranteed to find it! If not, you'll eventually end up back where you started, having explored all paths next to that wall.
Think of it like this: if all the walls are connected, you can imagine stretching them out into a big circle. Then, following the wall is just like walking around that circle from start to finish.
What if the maze isn't simple? This method doesn't work if the maze has loops that aren't connected to the main outer walls. For example, if you start in the middle of a maze with a path that loops back on itself, you might get stuck in that loop forever.
It's also important to start this method right at the maze entrance. If you start somewhere in the middle, you might find yourself stuck in a small loop of walls that doesn't lead to an exit. If this happens, you might need to try a different wall or switch to another method, like the Pledge Algorithm.
You can even use wall following in 3D mazes, but it's a bit trickier. You need to know which way is "left" or "right" in that 3D space.
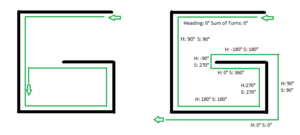
Pledge Algorithm
Sometimes, a maze might have parts that are completely separate from each other. If you start inside one of these separate sections, the wall follower method might just make you walk in circles. The Pledge algorithm helps solve this problem. It was created by Jon Pledge.
Here’s how it works: 1. Pick a main direction you want to go (like North). 2. Start walking in that direction. 3. If you hit an obstacle (a wall), put one hand (say, your right hand) on the wall. 4. Follow the wall, but also keep track of how much you turn. Turning clockwise is positive, counter-clockwise is negative. 5. Keep following the wall until you are facing your original chosen direction again and the total amount you've turned adds up to zero. 6. Once both conditions are met, leave the wall and continue walking in your original direction.
This method helps you get out of tricky spots, like a maze shaped like the letter "G". It makes sure you don't get stuck in a loop. The Pledge algorithm can help you find your way from any spot inside a maze to an exit on the outside. However, it won't help you find a specific goal inside the maze if you start from the outside.
Trémaux's Algorithm
Trémaux's algorithm was invented by Charles Pierre Trémaux. It's a smart way to find your way out of any maze, as long as the paths are clear. It's not guaranteed to find the shortest path, but it will always find a path. This method requires you to mark the paths as you go.
Here are the rules:
- Mark paths: Every time you walk down a path, mark it once. Make sure the mark is visible from both ends of the path.
- Avoid double-marked paths: Never go down a path that already has two marks on it.
- New junction: If you arrive at a place where paths meet (a junction) and none of the paths (except the one you just came from) have any marks, pick any unmarked path, walk down it, and mark it.
- Already explored junction: If you arrive at a junction and the path you just came from only has one mark, turn around and go back the way you came, marking that path a second time. This is what you do when you hit a dead end.
- Other paths: If the path you came from already has two marks, or if you're at a junction with other marked paths, choose the path with the fewest marks (zero if possible, otherwise one), walk down it, and mark it.
This "turn around and return" rule is very important. It helps you avoid getting stuck in loops and makes sure you explore all parts of the maze.
Once you find the exit, the path back to the start will be made up of all the paths you marked exactly once. If there's no exit, this method will lead you back to the start, and all paths will be marked twice.
This algorithm, discovered in the 1800s, is very similar to a modern computer search method called "depth-first search."
Dead-End Filling
Dead-end filling is a method for solving mazes that works best on paper or with a computer. It's not useful if you're actually inside an unknown maze because it requires you to see the whole maze at once.
Here's how it works: 1. Find all the "dead ends" in the maze. These are paths that lead nowhere. 2. "Fill in" or block off the path from each dead end until you reach the first junction. 3. Keep repeating this process. Sometimes, blocking off one dead end will create new dead ends that you can then fill in.
This method can't accidentally block off the correct path from the start to the finish. When you're done, only the correct path (or paths, if there are many) will be left unfilled. If the maze has no loops, only the shortest solution will remain.
Shortest Path Algorithm
When a maze has many possible ways to get from start to finish, you might want to find the shortest path. There are several computer methods to do this, often based on graph theory.
One common method is called a "breadth-first search." Imagine you're exploring the maze layer by layer. You start at the beginning and find all the paths you can reach in one step. Then, from those spots, you find all the paths you can reach in two steps, and so on. You keep track of how far each spot is from the start.
When you finally reach the finish line, you can trace your steps backward from the finish to the start, following the path that always got you closer. This backward path will be the shortest way!
Images for kids