NP-completeness facts for kids
NP-complete problems are a special group of problems in computer science. Imagine you have a puzzle. For some puzzles, it's easy to check if a solution is correct, but very hard to find the solution in the first place. NP-complete problems are like the hardest puzzles in this group.
The "NP" in NP-complete stands for "Nondeterministic Polynomial time." This means that if you have a possible answer to one of these problems, you can check if it's correct very quickly. "Quickly" in computer science means in "polynomial time," which is a way of saying the time it takes doesn't grow too fast as the problem gets bigger.
The "complete" part means these problems are connected. If you find a fast way to solve just one NP-complete problem, you could use that method to solve all other problems in the "NP" group quickly! This is why computer scientists are so interested in them.
Even though it's easy to check answers, finding the answers to NP-complete problems is very difficult with today's computers. As the problem gets larger, the time needed to find a solution grows incredibly fast. This big question—can we find solutions to these problems quickly?—is known as the P versus NP problem. It's one of the biggest unsolved mysteries in computer science, and there's even a million-dollar prize for anyone who solves it!
Contents
What Makes a Problem NP-Complete?
A problem is called NP-complete if it meets two main conditions:
- Easy to Check: If someone gives you a possible solution, you can quickly check if it's correct. Think of it like checking if a key fits a lock.
- Hardest in its Group: Every other problem that's easy to check can be changed into this problem relatively quickly. This means if you can solve this one fast, you can solve all the others fast too!
Problems that are "easy to check" are part of a group called NP. Problems that are "hardest in their group" are called NP-hard. So, an NP-complete problem is one that is both in NP and is NP-hard.
History of NP-Complete Problems
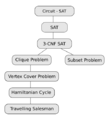
The idea of NP-completeness first appeared in 1971, thanks to a computer scientist named Stephen Cook. He proved that a problem called the Boolean satisfiability problem (often called SAT) was NP-complete. This was a huge discovery because it showed that such "hardest" problems actually exist!
Soon after, in 1972, Richard Karp showed that many other well-known problems were also NP-complete. This proved that NP-complete problems weren't just a single odd case, but a whole family of important problems. Since then, thousands of other problems have been shown to be NP-complete.
Examples of NP-Complete Problems
Many real-world problems that computer scientists and programmers face are NP-complete. Here are a few famous examples:
- Boolean Satisfiability Problem (SAT): Imagine you have a puzzle with many true/false statements, and you need to figure out if there's a way to make all of them true at the same time.
- Knapsack Problem: You have a knapsack and a list of items, each with a weight and a value. You want to pick items to put in your knapsack to get the highest total value, but you can't go over the weight limit.
- Travelling Salesman Problem: A salesman needs to visit several cities and return home. What's the shortest route that visits each city exactly once?
- Graph Coloring Problem: You have a map, and you want to color each region so that no two neighboring regions have the same color. What's the smallest number of colors you need?
These problems often seem simple to describe, but finding the best solution for large versions of them can be incredibly difficult.
How to Deal with NP-Complete Problems
Since there's no known quick way to find the perfect solution for NP-complete problems, computer scientists use different strategies:
- Approximation: Instead of finding the absolute best solution, they look for a solution that's "good enough" or very close to the best. This can be found much faster.
- Heuristics: These are clever tricks or rules of thumb that often work well in practice, even if they don't guarantee the perfect solution every time. They're like shortcuts that usually get you close to the right answer.
- Restriction: Sometimes, if you make the problem a bit simpler (for example, by limiting the number of cities in the Travelling Salesman Problem), it becomes easier to solve.
- Randomization: Using a bit of randomness can sometimes help find a good solution faster on average, though it might not always work perfectly.
Even though NP-complete problems are challenging, understanding them helps us know the limits of what computers can do quickly and guides us in finding practical ways to solve important problems.
Common Misunderstandings
It's easy to misunderstand NP-complete problems. Here are a few common myths:
- "NP-complete problems are the hardest problems ever." Not true! While they are very hard, some problems are even harder. For example, the halting problem is a problem that computers can never solve for all cases.
- "Solving NP-complete problems always takes a super long time." We don't know for sure! If someone proves P=NP, then they could be solved quickly. Even now, some NP-complete problems can be solved faster than others, or some specific versions of them might be easy.
- "A super powerful quantum computer could solve all NP-complete problems easily." This is also not true. While quantum computers are amazing, they are not expected to solve all NP-complete problems quickly.
Images for kids
-
The Boolean satisfiability problem (SAT) asks if a puzzle with true/false statements can be made true. It's easy to check an answer, but hard to find one.
-
This diagram shows how different types of problems relate to each other. NP-complete problems are a special group within NP.
-
This chart shows how some NP-complete problems are connected, meaning if you can solve one, you can often use that to help solve another.
See also
In Spanish: NP-completo para niños
