Ordered pair facts for kids
An ordered pair is a way to group two things together where the order really matters. Think of it like putting on your socks and then your shoes – the order is important!
In math, an ordered pair has a "first" item and a "second" item. We usually write it like this: (a,b). Here, 'a' is the first item, and 'b' is the second item. Sometimes you might see it written as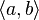 
.
The "ordered" part is super important. If the two items are different, then the pair (a,b) is not the same as (b,a). For example, (apple, banana) is different from (banana, apple).
Contents
What Makes Ordered Pairs Equal?
Imagine you have two ordered pairs, like (first item, second item) and (another first item, another second item).
The main rule for ordered pairs is this: An ordered pair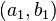 
is exactly the same as another ordered pair 
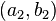only if:
- The first items are equal (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a_1 = a_2 )
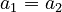- AND the second items are equal (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): b_1 = b_2 )
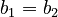So, if you have (5, 10) and (x, y), for them to be equal, 'x' must be 5 and 'y' must be 10. You can't have (5, 10) be equal to (10, 5) because the order is different!
Real-World Examples
Ordered pairs are used all the time!
- Coordinates on a map: When you look at a map, you might see coordinates like (latitude, longitude). The order matters a lot! (34N, 118W) is a specific place, and (118W, 34N) would be somewhere completely different.
- Game scores: In a game, if Team A scores 3 points and Team B scores 2 points, the score could be (3, 2). This is different from (2, 3), where Team B scored more.
- Dates: A date like (Month, Day) is an ordered pair. (July, 4) is different from (4, July) (which doesn't make sense as a date!).
How Mathematicians Define Them
Mathematicians like to be very precise. They have special ways to define an ordered pair using something called "sets." A famous mathematician named Kazimierz Kuratowski came up with a clever way to define an ordered pair (a,b) using sets. While the exact definition can look a bit complicated, the important thing is that it works perfectly to make sure the "order matters" rule is always true.
See also
- In Spanish: Par ordenado para niños
