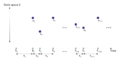kids encyclopedia robot

Poisson point process facts for kids

Kids Encyclopedia Facts

A Poisson process is a way to count how often certain events happen over time. Imagine you're watching something, like how many times a specific bird lands on your feeder, or how many phone calls a call center gets in an hour. A Poisson process helps us understand these kinds of events, especially when they happen randomly and independently of each other. It's a type of stochastic process, which means it deals with things that change randomly over time.

What is a Poisson Process?

A Poisson process is like a special kind of counting process. It keeps track of how many times an event occurs up to a certain point in time. Think of it like a tally counter for random events.

Here are the main ideas that define a Poisson process:

  • Starting Point: At the very beginning (time zero), no events have happened yet. We write this as N(0) = 0.
  • Independent Events: What happens in one time period doesn't affect what happens in another time period. For example, if you count calls from 1 PM to 2 PM, that count won't change how many calls happen from 3 PM to 4 PM. These are called "independent increments."
  • Random Occurrences: The number of events that happen in any specific amount of time (like 10 minutes or an hour) follows a special pattern called a Poisson distribution. This distribution helps us predict the chances of seeing a certain number of events.

N(t) simply means the total number of events that have happened by time 't'.

Real-World Examples

Poisson processes are used in many real-life situations:

  • Phone Calls: How many calls a customer service center receives in an hour.
  • Website Visits: The number of visitors arriving at a website per minute.
  • Natural Events: The number of earthquakes in a region over a year, or lightning strikes during a storm.
  • Technology: Even the way mobile phone towers are placed in a city can sometimes be described by a Poisson process, as seen in places like Sydney, Australia.

Images for kids

  • Sydney skyline at dusk - Dec 2008

    According to one study, the locations of mobile phone towers in Sydney, Australia, pictured above, can be like a Poisson process.

  • Marked point process

    This picture shows a "marked point process." If the original events are a Poisson process and the "marks" (extra information) are random, then the whole thing can still be a Poisson process.

See also

Kids robot.svg In Spanish: Proceso de Poisson para niños

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Poisson point process Facts for Kids. Kiddle Encyclopedia.