Polynomial root facts for kids

A root of a polynomial is a special number that makes the whole polynomial equal to zero when you plug it in. Think of a polynomial as a math puzzle, and the root is the secret key that solves it by making it zero!

For example, imagine the polynomial 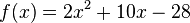. If you put the number 2 in place of x, it looks like this: 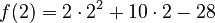Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): f(2) = 2\cdot 2^2 + 10\cdot 2 - 28 . When you do the math, you get 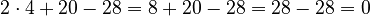Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2\cdot 4 + 20 - 28 = 8 + 20 - 28 = 28 - 28 = 0 . Since the answer is 0, the number 2 is a root of this polynomial! Another root for this same polynomial is -7.

What is a Polynomial Root?

A polynomial is a math expression made of variables (like x), numbers, and exponents (like the little 2 in 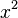). These are all joined by adding, subtracting, and multiplying. A root of a polynomial is simply a value for the variable that makes the entire expression equal to zero. It's like finding the "zero point" for that math equation.

Understanding Polynomials

Polynomials are super useful in many areas of math and science. They can have one term, like 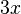, or many terms, like 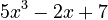Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 5x^3 - 2x + 7 . Each part of a polynomial is called a "term." The highest exponent in a polynomial tells you its "degree." For example, 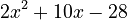Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2x^2 + 10x - 28 is a second-degree polynomial because the highest exponent is 2.

Why Finding Roots Matters

Finding the roots of a polynomial is important because it helps us solve many real-world problems. For instance, if a polynomial describes the path of a thrown ball, its roots could tell you when the ball hits the ground (where its height is zero). In engineering, economics, and even video game design, polynomials help model situations, and their roots provide key solutions.

How to Find Roots

There are different ways to find the roots of a polynomial, depending on its degree:

• Factoring: For some polynomials, you can break them down into simpler parts (factors). If you can factor a polynomial, setting each factor to zero will give you the roots.
• Quadratic Formula: For second-degree polynomials (like 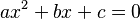Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): ax^2 + bx + c = 0 ), there's a special formula called the quadratic formula that always gives you the roots.
• Graphing: You can also graph a polynomial. The points where the graph crosses the x-axis (the horizontal line) are the roots! This is because at these points, the value of the polynomial (which is the y-value) is zero.
• Numerical Methods: For more complex polynomials, people use computers and special math methods to find approximate roots.

Real-World Examples

Polynomials and their roots are used in many cool ways:

• Physics: To calculate the trajectory of rockets or the motion of objects.
• Engineering: To design bridges, buildings, and roller coasters, making sure they are stable.
• Economics: To model supply and demand or predict financial trends.
• Computer Graphics: To create smooth curves and shapes in animations and games.