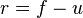Rank correlation facts for kids

A rank correlation helps us understand how two different lists of "rankings" are related. A ranking is simply putting things in order, like "first," "second," or "third." For example, if you rank your favorite video games, that's a ranking! A rank correlation coefficient is a number that shows how similar two different rankings are.

Imagine you want to know if colleges with a top-ranked basketball team also tend to have a top-ranked football team. Or, you might wonder if people with more education usually earn higher incomes. Rank correlation can help answer these kinds of questions.

Some common ways to measure rank correlation include:

• Spearman's ρ
• Kendall's τ
• Goodman and Kruskal's γ

The rank correlation coefficient is a number between -1 and 1.

• If the number is 1, it means the two rankings are exactly the same. They agree perfectly.
• If the number is 0, it means the rankings are completely unrelated. There's no connection between them.
• If the number is -1, it means the rankings are perfectly opposite. If one list goes up, the other goes down.

What is the Kerby Simple Difference Formula?

Dave Kerby suggested a simple way to understand rank correlation, especially for students. It's called the rank-biserial measure. This method looks at how much of your information supports an idea, and how much doesn't.

The Kerby simple difference formula says that rank correlation is the difference between the percentage of "favorable" evidence (f) and "unfavorable" evidence (u).

This means you subtract the "unfavorable" percentage from the "favorable" percentage.

How Does the Formula Work?

Let's look at an example to make this clearer. Imagine a coach trains long-distance runners using two different methods for a month.

• Group A has 5 runners.
• Group B has 4 runners.

The coach thinks method A will make runners faster. After a race, here are the results:

• Runners from Group A got ranks: 1, 2, 3, 4, and 6. (These are the faster runners).
• Runners from Group B got ranks: 5, 7, 8, and 9. (These are the slower runners).

To use the Kerby formula, we compare every runner from Group A with every runner from Group B. We make "pairs."

• For example, the fastest runner (rank 1 from Group A) is paired with all runners from Group B: (1,5), (1,7), (1,8), and (1,9).
• All these pairs support the coach's idea. In each pair, the Group A runner is faster than the Group B runner.

There are a total of 20 possible pairs (5 runners in Group A multiplied by 4 runners in Group B).

• 19 of these pairs support the coach's idea.
• Only one pair does not support the idea: the runners with ranks 5 (from Group B) and 6 (from Group A). In this case, the Group B runner was faster.

Using the Kerby formula:

• 95% of the data supports the idea (19 out of 20 pairs). So, f = 0.95.
• 5% of the data does not support the idea (1 out of 20 pairs). So, u = 0.05.
• The rank correlation is r = 0.95 - 0.05 = 0.90.

A correlation of r = 1 means that 100% of the pairs support the idea. This shows a perfect relationship. A correlation of r = 0 means that half the pairs support the idea and half do not. This shows no relationship between the groups and their ranks.