Rationalisation (mathematics) facts for kids
Root rationalisation is a way to make fractions look simpler by getting rid of square roots (or other roots) from the bottom part of the fraction. The bottom part of a fraction is called the denominator.
Imagine you have a fraction like 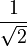 . It's often easier to work with this fraction if the square root is not in the denominator. Rationalisation helps us move that root to the top part (the numerator) or remove it completely from the fraction.
. It's often easier to work with this fraction if the square root is not in the denominator. Rationalisation helps us move that root to the top part (the numerator) or remove it completely from the fraction.
When the denominator has a single square root, like 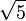 , you multiply both the top and bottom of the fraction by that same square root. This works because multiplying a square root by itself makes the root disappear (for example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5} \cdot \sqrt{5} = 5 ).
, you multiply both the top and bottom of the fraction by that same square root. This works because multiplying a square root by itself makes the root disappear (for example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5} \cdot \sqrt{5} = 5 ).
If the denominator has a sum or difference involving a square root, like 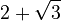 , you use a special trick. You multiply both the top and bottom by something called the "conjugate." The conjugate is the same expression but with the opposite sign in the middle (so for
, you use a special trick. You multiply both the top and bottom by something called the "conjugate." The conjugate is the same expression but with the opposite sign in the middle (so for 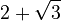 , the conjugate is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2 - \sqrt{3} ). This trick uses a math rule called the "difference of two squares" which helps the square roots disappear from the denominator.
, the conjugate is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2 - \sqrt{3} ). This trick uses a math rule called the "difference of two squares" which helps the square roots disappear from the denominator.
Contents
Rationalising a Single Square Root or Cube Root
To rationalise a fraction, you always multiply the numerator and the denominator by the same number or expression. This is like multiplying by 1, so it doesn't change the value of the fraction.
Example 1: Square Root
Let's look at this fraction:
To get rid of the 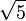 in the denominator, we multiply both the top and bottom by
in the denominator, we multiply both the top and bottom by 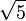 :
:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10}{\sqrt{5}} = \frac{10}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}}
Now, we multiply the numerators together and the denominators together:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}} = \frac{10\sqrt{5}}{(\sqrt{5})^2}
Since Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (\sqrt{5})^2 means 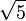 multiplied by itself, it equals 5.
multiplied by itself, it equals 5.
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10\sqrt{5}}{5}
Finally, we can simplify the numbers:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10\sqrt{5}}{5} = 2\sqrt{5}
The square root is now gone from the denominator!
Example 2: Cube Root
What if we have a cube root, like Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{a} ? Let's try this fraction:
To make a cube root disappear, you need to multiply it by itself two more times. So, we multiply by ![\sqrt[3]{a}^2](/images/math/1/c/b/1cb16cfdcb65e935ac33459ddf40f155.png) (which is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{a} \cdot \sqrt[3]{a} ):
(which is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{a} \cdot \sqrt[3]{a} ):
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10}{\sqrt[3]{a}} = \frac{10}{\sqrt[3]{a}} \cdot \frac{\sqrt[3]{a}^2}{\sqrt[3]{a}^2}
Multiply the top and bottom:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10 \cdot \sqrt[3]{a}^2}{\sqrt[3]{a} \cdot \sqrt[3]{a}^2} = \frac{10\sqrt[3]{a}^2}{\sqrt[3]{a}^3}
Since Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{a}^3 means Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt[3]{a} multiplied by itself three times, it equals a.
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{10\sqrt[3]{a}^2}{a}
The cube root is now gone from the denominator!
Dealing with More Square Roots
When the denominator has two terms, one or both of which are square roots, we use a special trick with something called a "conjugate."
If you have an expression like Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{2} + \sqrt{3} , its conjugate is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{2} - \sqrt{3} . The only difference is the sign in the middle.
When you multiply an expression by its conjugate, you use the "difference of two squares" rule: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (x+y)(x-y) = x^2 - y^2 . This rule is very helpful because it makes the square roots disappear!
Example 1: Two Square Roots
Let's rationalise this fraction:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3}{\sqrt{3}+\sqrt{5}}
The denominator is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{3}+\sqrt{5} . Its conjugate is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{3}-\sqrt{5} . We multiply both the top and bottom by the conjugate:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3}{\sqrt{3}+\sqrt{5}} \cdot \frac{\sqrt{3}-\sqrt{5}}{\sqrt{3}-\sqrt{5}}
Now, multiply the numerators and the denominators:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3(\sqrt{3}-\sqrt{5})}{(\sqrt{3}+\sqrt{5})(\sqrt{3}-\sqrt{5})}
For the denominator, we use the difference of two squares rule: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (\sqrt{3})^2 - (\sqrt{5})^2 .
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3(\sqrt{3}-\sqrt{5})}{3 - 5}
Simplify the denominator:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3(\sqrt{3}-\sqrt{5})}{-2}
This is the rationalised form of the fraction.
Example 2: Square Root with an Imaginary Number
This process also works with complex numbers that involve 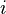 , where
, where 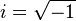 . Let's rationalise this fraction:
. Let's rationalise this fraction:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7}{1+\sqrt{-5}}
Remember that Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{-5} can be written as Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{5}i . So the denominator is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1+\sqrt{5}i . The conjugate of Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1+\sqrt{-5} is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1-\sqrt{-5} . We multiply both the top and bottom by the conjugate:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7}{1+\sqrt{-5}} \cdot \frac{1-\sqrt{-5}}{1-\sqrt{-5}}
Multiply the numerators and the denominators:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7(1-\sqrt{-5})}{1^2 - (\sqrt{-5})^2}
Now, simplify the denominator. Remember that Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (\sqrt{-5})^2 = -5 .
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7(1-\sqrt{-5})}{1 - (-5)}
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7(1-\sqrt{-5})}{1 + 5}
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7(1-\sqrt{-5})}{6}
This can also be written as:
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{7 - 7\sqrt{5}i}{6}
See also



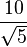
![\frac{10}{\sqrt[3]{a}}](/images/math/f/2/d/f2dd75b2931f9aeef0a1798b86794e9c.png)