Simply connected space facts for kids
A shape or "space" is called simply connected if you can draw any loop inside it and then shrink that loop down to a single point, without ever leaving the shape. Think of it like a rubber band. If you stretch a rubber band inside a shape, can you always pull it tighter and tighter until it's just a tiny dot, without the rubber band ever going outside the shape? If yes, the shape is simply connected!
Contents
What is a Simply Connected Space?
A simply connected space is a special kind of shape. It means it has no "holes" or "gaps" that go all the way through it. If you pick any two points inside the shape, you can always draw a path between them. More importantly, any closed loop you draw inside the shape can be smoothly shrunk to a single point.
Imagine a Rubber Band
Let's use the rubber band idea. Imagine you have a rubber band. You place it inside a shape. If you can always pull that rubber band smaller and smaller until it becomes a tiny dot, without it ever leaving the shape, then the shape is simply connected. If the rubber band gets stuck around a hole, then the shape is not simply connected.
Examples of Simply Connected Shapes
Many common shapes are simply connected.
- A solid ball or a sphere (like a basketball) is simply connected. You can draw any loop on its surface or inside it. You can always shrink that loop to a point.
- A solid cube is also simply connected.
- A flat piece of paper (a disk) is simply connected.
Shapes That Are NOT Simply Connected
Some shapes have holes that prevent them from being simply connected.
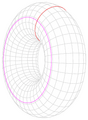
- A donut (or a torus) is a great example. If you draw a loop around the hole of the donut, you cannot shrink that loop to a point without leaving the donut's surface. The hole gets in the way.
- A ring or a washer shape is also not simply connected. It has a hole in the middle.
- A coffee cup with a handle is not simply connected because of the hole in its handle.
The Torus (Donut Shape)
The torus is a classic example of a shape that is not simply connected. If you draw a loop that goes around the "hole" of the donut, you can't make that loop disappear without cutting the donut or lifting the loop off its surface. This is because the hole prevents the loop from shrinking completely.
Why is This Important?
The idea of "simply connected" spaces is very important in a part of mathematics called Topology. Topology studies the properties of shapes that stay the same even if you stretch, twist, or bend them. Understanding if a space is simply connected helps mathematicians classify and understand different shapes. It's used in many areas, from understanding the universe to designing computer graphics.
Images for kids
-
A sphere is simply connected because every loop can be shrunk to a point on its surface.
-
A torus (donut shape) is not simply connected. The colored loops cannot shrink to a point without leaving the surface.
See also
In Spanish: Conjunto simplemente conexo para niños
