kids encyclopedia robot

Synthetic division facts for kids

Kids Encyclopedia Facts

Synthetic division is a quick and easy way to divide polynomials. It's like a shortcut compared to polynomial long division. This method is super helpful when you need to divide a polynomial by a simple expression like x - a.

Even though it's often used for x - a type problems, you can use synthetic division for any polynomial that only has one variable. It helps you do math without writing out all the variables, saving space and time. Plus, it changes subtractions into additions, which can help prevent mistakes.

When you use synthetic division for these simple division problems, it's also known as a part of Ruffini's rule.

How to do Synthetic Division

Let's learn how to do synthetic division with an example. We will divide a polynomial by a simple expression like x - a.

Setting Up Your Division Problem

Imagine you want to solve this problem: 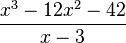\frac{x^3 - 12x^2 - 42}{x - 3}

First, write down the numbers in front of each term of the top polynomial. If a term is missing (like x in this example), use a zero as its number.

  • For 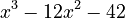Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^3 - 12x^2 - 42 , the numbers are 1 (for 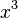x^3), -12 (for 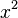x^2), 0 (for the missing x term), and -42 (for the number without x).

You'll set it up like this: 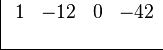\begin{array}{cc} \begin{array}{r} \\ \\ \end{array} & \begin{array}{|rrrr} \ 1 & -12 & 0 & -42 \\ & & & \\ \hline \end{array} \end{array}

Next, look at the bottom part of your division problem, which is 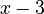Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x - 3 . Take the number from this part and change its sign. So, for 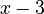Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x - 3 , you'll use positive 3.

  • Place this number to the left of your setup:

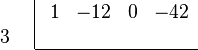
\begin{array}{cc} \begin{array}{r} \\ 3 \\ \end{array} & \begin{array}{|rrrr} \ 1 & -12 & 0 & -42 \\ & & & \\ \hline \end{array} \end{array}

Performing the Steps

Now, let's do the math!

  1. Bring Down the First Number: Take the very first number from the top row (which is 1) and bring it straight down below the line.

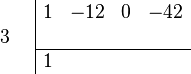
\begin{array}{cc} \begin{array}{r} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & & & \\ \hline 1 & & & \\ \end{array} \end{array}

  1. Multiply and Place: Multiply the number you just brought down (1) by the number on the far left (3). Put the answer (3) under the next number in the top row (-12).

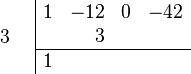
\begin{array}{cc} \begin{array}{r} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & 3 & & \\ \hline 1 & & & \\ \end{array} \end{array}

  1. Add the Column: Add the numbers in the second column (-12 and 3). Write the sum (-9) below the line.

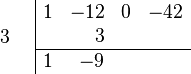
\begin{array}{cc} \begin{array}{c} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & 3 & & \\ \hline 1 & -9 & & \\ \end{array} \end{array}

  1. Repeat the Process: Keep doing steps 2 and 3 for the rest of the numbers.
  • Multiply -9 by 3 to get -27. Place -27 under 0.
  • Add 0 and -27 to get -27.
  • Multiply -27 by 3 to get -81. Place -81 under -42.
  • Add -42 and -81 to get -123.

Your setup will now look like this: 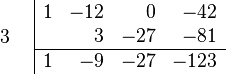\begin{array}{cc} \begin{array}{c} \\ 3 \\ \\ \end{array} & \begin{array}{|rrrr} 1 & -12 & 0 & -42 \\ & 3 & -27 & -81 \\ \hline 1 & -9 & -27 & -123 \end{array} \end{array}

Understanding Your Answer

The numbers below the line are the numbers for your answer. The very last number is your remainder.

  • Draw a line before the last number to show it's the remainder:

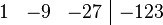
\begin{array}{rrr|r} 1 & -9 & -27 & -123 \end{array}

Now, turn these numbers back into a polynomial. Start from the right of the remainder line.

  • The number just before the remainder (-27) is the constant term (no x).
  • The next number to the left (-9) is the coefficient for x.
  • The next number to the left (1) is the coefficient for x^2.

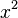So, your answer looks like this: \begin{array}{rrr|r} 1x^2 & -9x & -27 & -123 \end{array}

This means the result of the division is 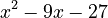Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2 - 9x - 27 , and you have a remainder of -123. You write the final answer as: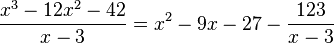 \frac{x^3 - 12x^2 - 42}{x - 3} = x^2 - 9x - 27 - \frac{123}{x - 3}

Synthetic division is a neat trick that makes dividing polynomials much faster and simpler!

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Synthetic division Facts for Kids. Kiddle Encyclopedia.