Algebraic solution facts for kids
An algebraic solution is a special way to find the answer to a math problem, called an algebraic equation. Imagine you have an equation with letters (like 'x' or 'y') and numbers. An algebraic solution gives you the answer for those letters using only basic math steps. These steps are:
- Adding numbers
- Subtracting numbers
- Multiplying numbers
- Dividing numbers
- Finding roots (like a square root, which is finding a number that, when multiplied by itself, gives you the original number, or a cube root, and so on).
The answer you get is an algebraic expression, which is a combination of numbers, letters, and math operations.
Contents
What is an Algebraic Equation?
An algebraic equation is a math sentence that says two things are equal. It usually has one or more unknown values, shown by letters (called variables). For example, in the equation `2x + 5 = 11`, 'x' is the variable. An algebraic solution helps you find what 'x' is.
Solving Quadratic Equations
One of the most famous examples of an algebraic solution is how we solve a quadratic equation. A quadratic equation is a type of equation where the highest power of the variable (like 'x') is 2 (so you see `x^2`).
A general quadratic equation looks like this: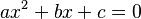 
(Here, 'a', 'b', and 'c' are numbers, and 'a' cannot be zero).
The algebraic solution for 'x' in this equation is given by the well-known quadratic formula: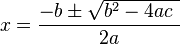 
This formula uses only addition, subtraction, multiplication, division, and a square root to find the values of 'x' that make the equation true.
Beyond Simple Equations
As equations get more complex, finding an algebraic solution can become much harder.
Cubic and Quartic Equations
For equations where the highest power of the variable is 3 (called a cubic equation) or 4 (called a quartic equation), there are also algebraic solutions. However, these solutions are much more complicated than the quadratic formula. They involve many more steps and roots.
The Challenge of Quintic Equations
When we get to equations where the highest power of the variable is 5 (called a quintic equation) or even higher (like 6, 7, etc.), something interesting happens. A very important idea in math, called the Abel-Ruffini theorem, tells us that for a general equation of degree 5 or higher, there isn't always an algebraic solution.
This means you can't always find the answer using only addition, subtraction, multiplication, division, and roots. It's not that we haven't found the formula yet; it's been proven that such a general formula doesn't exist for these types of equations.
However, it's important to know that this applies to *general* equations. Some specific equations of degree 5 or higher *can* still be solved algebraically. For example, if you have an equation like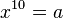 
, you can easily find the solution as 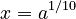Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x=a^{1/10} (which means the tenth root of 'a').
See also
In Spanish: Solución algebraica para niños
