Basis (linear algebra) facts for kids
In linear algebra, a basis is like a special set of building blocks for vectors. Imagine vectors as arrows that have both a length and a direction. A vector space is simply a collection of all these possible arrows.
A basis is a set of vectors that has two important features:
- You can create any other vector in that space by combining these basis vectors. This means you multiply each basis vector by a number and then add them all together.
- If you remove even one vector from this special set, you won't be able to create all the other vectors in the space anymore. Each basis vector is essential.
The dimension of a vector space is simply the number of vectors in its basis. For example, our everyday world is 3D, meaning it has a basis of three vectors.
Contents
What is a Basis?
A basis helps us understand and describe any vector within a specific vector space. Think of it like a coordinate system. When you give directions, you might say "go 3 steps east and 2 steps north." Here, "east" and "north" are like your basis vectors. You can describe any location on a flat map using just these two directions.
Building Blocks for Vectors
The first rule for a basis is that its vectors must be able to "span" the entire space. This means that by using different amounts of each basis vector (multiplying them by numbers) and adding them up, you can reach any other vector in that space. It's like having a set of LEGO bricks that can build any structure you can imagine.
Essential Vectors
The second rule is about being "linearly independent." This means that none of the basis vectors can be made by combining the other basis vectors. Each vector in the basis is unique and necessary. If you could make one basis vector from the others, it would be redundant, and you could remove it without losing the ability to create all other vectors.
Example of a Basis
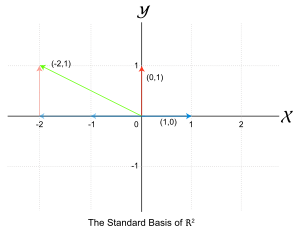
Let's look at a simple example using a 3D space, like the world around us. In this space, every point or arrow can be described using three numbers, like (x, y, z).
A very common basis for this 3D space is the set of three vectors:
- (1, 0, 0) - This is an arrow pointing along the X-axis.
- (0, 1, 0) - This is an arrow pointing along the Y-axis.
- (0, 0, 1) - This is an arrow pointing along the Z-axis.
How it Works
Imagine you have an arrow that points to (5, 3, 2). You can create this arrow by combining our basis vectors:
- Take 5 times the (1, 0, 0) vector: This gives you (5, 0, 0).
- Take 3 times the (0, 1, 0) vector: This gives you (0, 3, 0).
- Take 2 times the (0, 0, 1) vector: This gives you (0, 0, 2).
Now, if you add these three new vectors together: (5, 0, 0) + (0, 3, 0) + (0, 0, 2) = (5, 3, 2).
This shows that you can indeed make any vector in 3D space using these three simple basis vectors. Also, you can't make (1,0,0) by combining (0,1,0) and (0,0,1), so they are essential. This makes them a perfect basis!
Images for kids
-
This image shows how different sets of vectors can be arranged in higher dimensions.
See also
In Spanish: Base (álgebra) para niños
