Vector space facts for kids
A vector space is like a special club for mathematical objects called vectors. In this club, you can do two main things with vectors: you can add them together, and you can multiply them by regular numbers (which we call scalars).
The cool thing about a vector space is that when you add two vectors from the club, or multiply a vector by a scalar, the answer is always another vector that still belongs to the same club. It's like a closed system! We often use letters like U, V, and W to stand for vector spaces.
Vectors are super important in a part of math called linear algebra. This area of math deals with straight lines and flat surfaces, not curvy ones.
Contents
What is a Vector?
Think of a vector as an arrow. This arrow has a starting point (its "tail") and an ending point (its "head"). It also has a certain length and points in a specific direction.
Adding Vectors
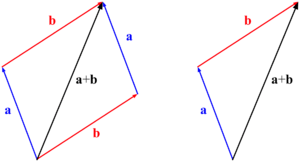
When you want to add two vectors, imagine placing the tail of the second vector at the head of the first vector. The new vector that goes from the tail of the first vector to the head of the second vector is their sum. The picture at the top of this page shows you how this works!
Multiplying Vectors by Numbers
Multiplying a vector by a scalar (a regular number) means changing its size. For example:
- If you multiply a vector by 2, you make it twice as long.
- If you multiply it by 1/2, you make it half as long.
- If you multiply it by a negative number, it flips around and points in the opposite direction!
What Else Can Be a Vector?
Sometimes, the "vectors" in a vector space aren't just arrows. They can be other mathematical things too, like:
- Functions (rules that turn one number into another)
- Matrices (grids of numbers)
- Even just regular numbers!
If these objects follow certain rules (called "axioms"), they can be treated like vectors. This means all the cool ideas and theorems from linear algebra will still work for them.
Finding a Basis
Imagine you have a special set of vectors. This set is called a basis if you can make any other vector in the space by adding these special vectors together and multiplying them by scalars. It's like having a basic building kit for all the vectors in the space!
Every vector space has at least one basis. Also, every basis for a particular vector space will always have the same number of vectors in it. This is a big idea in math called the dimension theorem.
Understanding Dimension
Because all bases of a vector space have the same number of vectors, we can use this number to define the dimension of the vector space. For example, a flat surface (like a piece of paper) is 2-dimensional because you need two basic directions (like "across" and "up") to describe any point on it.
Related pages
Images for kids
-
The succeeding snapshots show summation of 1 to 5 terms in approximating a periodic function (blue) by finite sum of sine functions (red).
-
The heat equation describes the dissipation of physical properties over time, such as the decline of the temperature of a hot body placed in a colder environment (yellow depicts colder regions than red).
See also
In Spanish: Espacio vectorial para niños
