Unit vector facts for kids
A unit vector is a special kind of vector that has a length of exactly one unit. Think of it like a tiny arrow that only tells you a direction, not how far to go.
Vectors are like arrows that show both direction and how long something is (its "magnitude"). A unit vector is super useful because it only focuses on the direction. It's like pointing your finger in a certain way – your finger's length doesn't matter, only the direction it's pointing.
You can turn any regular vector into a unit vector by dividing it by its own length. This makes sure the new vector has a length of one, but it still points in the exact same direction as the original vector.
What are Unit Vectors?
A unit vector is a vector with a magnitude (length) of 1. It helps us describe direction.
- Imagine you have a vector that points from your house to the park, and it's 5 blocks long.
- The unit vector for this would be a tiny vector, just 1 block long, that still points exactly from your house to the park.
Unit vectors are often written with a little "hat" symbol over the letter, like 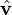Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \hat{\mathbf{v}} . This helps you know it's a unit vector.
Unit Vectors in 3D Space
In 3D space, we often use three special unit vectors to describe directions along the main axes:
- i (or
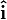): This unit vector points along the x-axis. - j (or
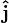): This unit vector points along the y-axis. - k (or
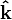): This unit vector points along the z-axis.
These are like the basic building blocks for describing any direction in a 3D world.
You can write them like this:
- i = (1, 0, 0) – meaning 1 unit along x, 0 along y, 0 along z.
- j = (0, 1, 0) – meaning 0 units along x, 1 along y, 0 along z.
- k = (0, 0, 1) – meaning 0 units along x, 0 along y, 1 along z.
Sometimes, people use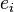 
or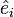 
to talk about unit vectors that form a "basis" (a set of basic directions) in a vector space.
Related pages
