Bisection method facts for kids
The bisection method is a clever way to find approximate solutions for certain math problems, especially when you're looking for a number that makes an equation true. Imagine you have a puzzle where you need to find a secret number. This method helps you get very, very close to that secret number!
Contents
Understanding Functions and Solutions
To use the bisection method, we first need to understand what a function is. In math, a function is like a machine that takes an input number (let's call it 'x') and gives you an output number (let's call it 'F(x)'). For example, if F(x) = x - 2, and you put in x=5, the output F(5) would be 3.
What is a Solution?
When we talk about a "solution" for a function F(x), we usually mean finding the 'x' value that makes F(x) equal to zero. Think about it like this: if you draw the graph of a function, the solution is where the line or curve crosses the horizontal 'x-axis'. At this point, the 'y' value (which is F(x)) is exactly zero.
How the Bisection Method Works
The bisection method helps us find these 'x' values. It's especially useful for continuous functions, which are functions whose graphs you can draw without lifting your pencil.
Finding a Starting Range
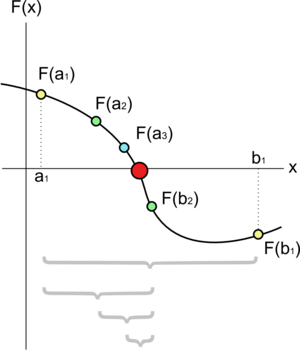
First, we need to pick a starting range. This range will have a lower number (let's call it 'a') and an upper number (let's call it 'b'). We then calculate F(a) and F(b). If F(a) and F(b) have different signs (one is positive and the other is negative), it means the function's graph must have crossed the x-axis somewhere between 'a' and 'b'. This tells us that our solution is definitely inside this range!
Halving the Range
To get a more precise answer, we need to make our range smaller. We do this by finding the middle point of our current range. Let's call this middle point 'c' (where c = (a+b)/2).
Now, we have two smaller ranges:
- From 'a' to 'c'
- From 'c' to 'b'
We then check which of these new, smaller ranges contains the solution. We do this by looking at the signs of F(a), F(c), and F(b).
- If F(a) and F(c) have different signs, the solution is in the range from 'a' to 'c'.
- If F(c) and F(b) have different signs, the solution is in the range from 'c' to 'b'.
We pick the range that contains the solution and ignore the other one.
Getting More Precise
We keep repeating this process:
- Find the middle point of the new, smaller range.
- Check which half of that range contains the solution.
- Make that half our new range.
We continue doing this until our range becomes incredibly small – so small that the difference between the lower and upper numbers is tiny, much smaller than the error we are willing to accept.
The Final Answer
Once the range is super small, we can take the middle point of this final tiny range as our estimated solution for F(x) = 0. It won't be the exact answer, but it will be very, very close! This method is simple and always works if you start with a range that truly contains a solution.
See also
 In Spanish: Método de bisección para niños
In Spanish: Método de bisección para niños