Chessboard paradox facts for kids
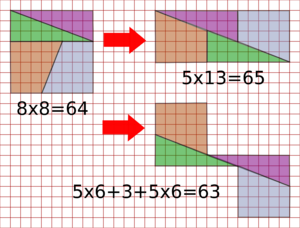
The chessboard paradox is a cool puzzle that tricks your eyes! It's also called the paradox of Loyd and Schlömilch. Imagine you have a chessboard, which is a square with sides 8 units long. Its total area is 64 square units (8 x 8).
Now, you cut this square into four special pieces. If you rearrange these four pieces, they seem to form a rectangle that is 13 units long and 5 units wide. If you multiply 13 by 5, you get 65 square units.
So, how can the same pieces make an area of 64 square units in one shape and 65 square units in another? This seems impossible! The trick is that the four pieces don't actually fit together perfectly in the rectangle. They leave a very tiny, almost invisible gap along the diagonal. This small gap is what makes the area seem to increase by one square unit.
This clever puzzle is sometimes credited to Sam Loyd, an American puzzle inventor, and Oskar Schlömilch, a German mathematician.
How the Illusion Works
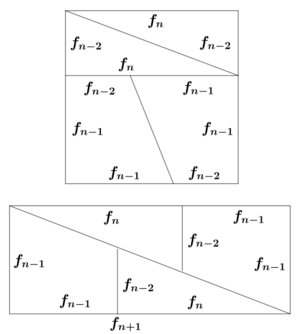
The secret behind this amazing illusion involves a special set of numbers called Fibonacci numbers. These numbers start with 0 and 1, and each new number is found by adding the two numbers before it (0, 1, 1, 2, 3, 5, 8, 13, 21, and so on).
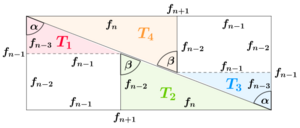
In the chessboard paradox, the lengths used to cut the square are often 2, 3, 5, 8, and 13. Notice that these are all Fibonacci numbers!
When you arrange the pieces to form the rectangle, the edges don't line up perfectly straight. Instead, they create a very thin, long, diamond-shaped gap in the middle. This gap is so narrow that it looks like a single line, making your eyes believe the pieces fit perfectly.
Making the Illusion Even Better
Mathematicians have found that the difference in area between the square and the rectangle is always exactly 1 square unit. This means that if the square has an area of 64, the rectangle will have an area of 65.
If you use larger Fibonacci numbers to create the puzzle, the tiny gap becomes even smaller and harder to see. For example, if you used a square with sides 21 units long (the next Fibonacci number after 13), the illusion would be even more convincing!
Sometimes, instead of a tiny gap, the pieces might slightly overlap. But the difference in area is still just 1 square unit. Because the gap or overlap gets smaller and smaller as you use larger numbers, the illusion becomes almost impossible to spot.
A Perfect Fit?
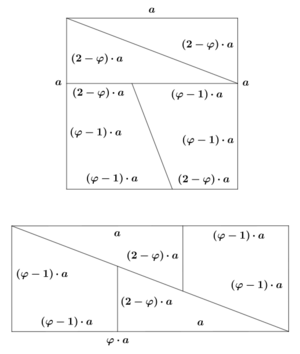
It is actually possible to cut a square into pieces that will fit together *exactly* to form a rectangle with the same area, without any gaps or overlaps. This perfect fit uses a special number called the golden ratio. The golden ratio is about 1.618, and it's found all over in nature and art.
When you use the golden ratio to decide how to cut the square, the pieces truly fit together perfectly. This means the area of the square and the area of the new rectangle will be exactly the same.