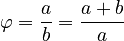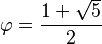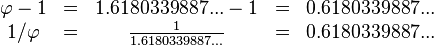Golden ratio facts for kids
The golden ratio is a special number that appears often in nature, art, and mathematics. It's about 1.618. We use the Greek letter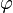 
(pronounced "phi") to represent it.
Imagine you have two numbers, a and b, where a is bigger than b. If you divide a by b, you get a ratio (a/b). Now, if you add a and b together, and then divide that sum by a, you get another ratio ((a+b)/a). If these two ratios are exactly the same number, then that number is the golden ratio!
So, if 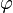is the golden ratio, then:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \varphi = \frac{a}{b} = \frac{a+b}{a}
This special number can also be written as:
This means 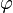is approximately 1.6180339887...
The golden ratio is an irrational number. This means its decimal part goes on forever without repeating any pattern. Even if you subtract 1 from it, or divide 1 by it, the number still goes on forever:
Contents
Golden Rectangle
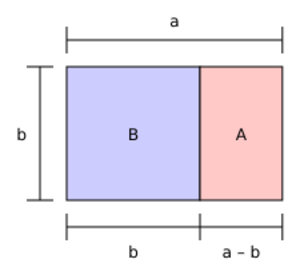
A "golden rectangle" is a rectangle where the length divided by the width equals the golden ratio. It looks very balanced and pleasing to the eye.
What's cool about a golden rectangle is that if you cut off a square from one end, the part that's left is another, smaller golden rectangle! This smaller rectangle has the exact same proportions as the original one.
In the picture, the big rectangle (blue and pink together) is a golden rectangle. The blue part (B) is a square. The pink part (A) is the new, smaller golden rectangle.
Fibonacci Numbers
The Fibonacci numbers are a famous list of numbers. You find the next number in the list by adding the two numbers before it. The list starts like this: 1, 1, 2, 3, 5, 8, 13, 21, and so on.
What's amazing is that if you divide any Fibonacci number by the one just before it, the answer gets closer and closer to the golden ratio!
| Fibonacci number | Divided by the one before | Ratio (approximate) |
|---|---|---|
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
|
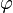= 1.6180... |
Golden Ratio in Nature
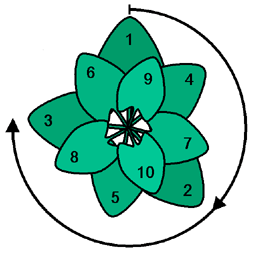
You can find the golden ratio in many places in nature. For example, it often shows up in the way leaves are arranged on a stem or how flower petals grow.
Plants often use a special angle called the golden angle, which is about 137.5 degrees. When leaves or flowers grow at this angle, they are arranged in a way that helps them get the most sunlight. This pattern helps them grow efficiently.
Related pages
Images for kids
-
Michael Maestlin was one of the first to write down the golden ratio as a decimal.
-
Dan Shechtman shows quasicrystals, which have patterns related to the golden ratio.
-
The golden ratio is connected to the roots of certain math equations.
-
You can get closer to the golden ratio by using fractions made from Fibonacci numbers.
-
The 600-cell is a complex 4D shape with proportions linked to the golden ratio.
-
This image shows how the golden ratio appears in advanced math, like the E8 group.
-
An illustration of a dodecahedron from a book by Luca Pacioli and Leonardo da Vinci.
-
The saucer plant, Aeonium tabuliforme, shows spiral patterns related to the golden ratio.
-
Nautilus shells have a spiral shape, often thought to be related to the golden ratio.
-
Some people believe the Great Pyramid of Giza uses the golden ratio in its design.
-
Many thought the Parthenon in Greece used the golden ratio, but this has been questioned.
-
Albert Gleizes used mathematical ideas, including the golden ratio, in his art.
See also
In Spanish: Número áureo para niños
