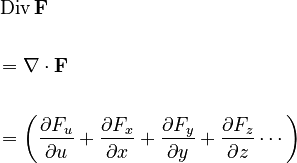Contour integral facts for kids

In complex analysis, contour integration is a special way to calculate an integral (which is like finding the total "amount" or "area" of something) around a path on the complex plane. Think of the complex plane as a special kind of graph where numbers have two parts: a real part and an imaginary part. So, contour integration is about adding up values of a function as you move along a specific path on this complex graph.

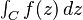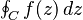When we write a contour integral, it looks like or . Here, 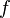is the function we are working with, and 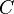is the path (or "contour") we are integrating along.

Using the Residue Theorem for Contour Integrals

One of the main ways to solve contour integrals is by using something called the residue theorem. This theorem gives us a clever shortcut to find the value of these integrals.

The residue theorem says that if you want to find the integral of a function 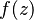around a closed path 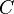, you can do it by looking at special points inside that path. These special points are where the function might behave strangely, and we call their "strength" or "value" at these points a residue.

The theorem basically tells us that the integral is equal to 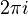Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2\pi i multiplied by the sum of these "residues" of the function inside the path 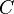. This makes calculating complex integrals much simpler than doing them step-by-step.

Contour Integrals with Many Variables

Sometimes, we need to calculate contour integrals for functions that depend on more than one variable. These are called multivariable contour integrals. They can include things like surface integrals or complex volume integrals.

To solve these more complex integrals, we often use another important rule called the divergence theorem. This theorem helps us change a difficult integral over a volume into a simpler integral over the surface that encloses that volume.

The divergence theorem connects the "flow" of a vector field (which is like a map showing direction and strength at every point) through a closed surface to the "sources" or "sinks" of that flow inside the volume. The "divergence" of a vector field tells us how much the field is spreading out or shrinking at a particular point.

The formula for divergence looks like this:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{align} &\operatorname{Div}{\mathbf{F}}\\\\ &=\nabla\cdot\textbf{F}\\\\ &= \left(\frac{\partial F_u}{\partial u} + \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\cdots \right) \end{align}

This formula helps us calculate how much a vector field is "diverging" (spreading out) at any point. By using the divergence theorem, we can turn a hard problem of integrating over a whole volume into an easier problem of integrating over its boundary surface.

Related pages

• Cauchy's integral formula
• Line integral

Images for kids

• 

  This diagram shows a contour, which is a path on the complex plane.

• 

  This is an example of a Hankel contour, another type of path used in complex integration.